Continuamos con la entrada dedicada a dar unas pequeñas nociones de sistemas de control automático en un procesador como Arduino. En esta entrada veremos el controlador PID, uno de los controladores más extendido por su sencillez y por ser capaz de conseguir un buen comportamiento en una gran variedad de situaciones.
En la primera entrada vimos algunas generalidades y definiciones sobre teoría de sistemas. En la segunda, vimos uno de los controles más sencillos, el control todo o nada con histéresis, así como sus limitaciones.
Por supuesto, insistimos en que no vamos a entrar en profundidad en los detalles del PID, dado que es tema muy extenso (e interesante). Si tenéis interés podéis consultar la abundante documentación disponible.
Aquí intentaremos dar una visión intuitiva del controlador y de la motivación que explica su comportamiento. Sin usar ecuaciones, ni matemáticas. De hecho, es una de las cosas geniales del PID, que no necesitas saber en detalle cómo funciona, para hacer que funcione.
¿Qué es el controlador PID?
El controlador PID es uno de los más empleados en la industria para el control de sistemas realimentados. Algunas de sus fortalezas son su sencillez y que es capaz de dar un buen comportamiento en una gran variedad de situaciones sin necesidad de conocer con detalle la planta a controlar.
El controlador PID es conocido desde hace tiempo. Sus primeros usos datan de 1911, y su primer análisis teórico de 1922 de la mano de Nicolas Minorsky. En esos tiempos, el control PID era exclusivamente analógico. Sin embargo, resulta fácil implementar en programación un PID digital y los cálculos que requiere son sencillos y eficientes. Además, es “relativamente sencillo” extrapolar la teoría de los PID analógicos a su equivalente digital.
Pese a su popularidad, debemos decir que actualmente en PID no es el mejor controlador disponible. Pero en la mayoría de los casos es más que suficiente. Por otro lado, muchos de los controladores más “modernos” no dejan de ser versiones mejoradas de un PID, como por ejemplo las distintas familias basadas en PID con parámetros adaptativos.
¿Cómo funciona el PID?
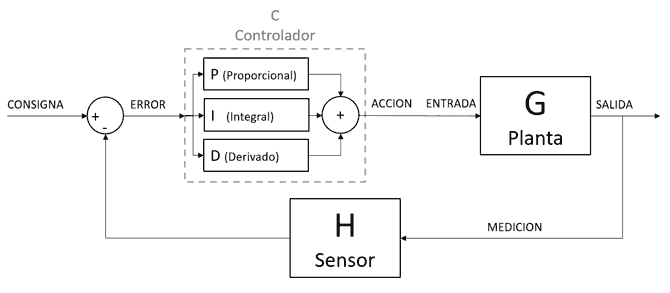
El algoritmo PID (proporcional, integral, derivado) está formado por la suma de tres componentes, Proporcional, Integral, y Derivado. Matemáticamente, un controlador PID tiene la siguiente formulación.
Un momento un momento. ¡Habíamos dicho sin ecuaciones! Bueno sí, pero no podemos hacer una entrada sobre PID sin ver al menos su formulación. Os prometo que no habrá más ¿vale?
Cada componente del PID es “independiente” de las demás, en el sentido de que cada uno calcula una salida de lo que “para el” deberías hacer para obtener la respuesta adecuada.
Los tres componentes se suman para dar la salida del controlador. Cada uno cumple una cierta función y mejoran cierta parte de la respuesta. Y cuando los tres componentes trabajan juntos, en la proporción adecuada, consiguen un gran comportamiento.
Cada componente tiene un parámetro Kp, Ki y Kd, respectivamente. Estos parámetros indican la ponderación (o “la fuerza”) que tiene en el resultado final. Que la respuesta del PID sea buena, cosas rotas, muerte, destrucción y despido, reside en el ajuste correcto de estos tres parámetros.
Y aquí viene la parte “graciosa” del PID. En los tres parámetros, si pones un valor muy bajo no se va a notar el efecto del componente en la salida. Y si lo pones demasiado alto… pues eso, muerte, destrucción, cosas rotas, etc.
Es más, en la respuesta global del controlador los tres componentes trabajan juntos e influyen uno sobre otros, por lo que no vale con ajustar cada uno de los parámetros de forma independiente. Existe una cierta “zona” dentro de los tres parámetros, donde el comportamiento es más o menos bueno.
Lógicamente, queda claro que la dificultad (que tampoco es para tanto) de un PID es ajustar los parámetros K, Ki y Kd, para que el comportamiento sea bueno. Y a eso dedicaremos la próxima entrada.
Explicando el PID
Para explicar el controlador PID vamos a continuar con nuestro ejemplo. Recordemos que en este caso tú eres el controlador y estás sentado en una sala. En la pared tienes dos displays, uno azul y uno rojo. También tienes una palanca.
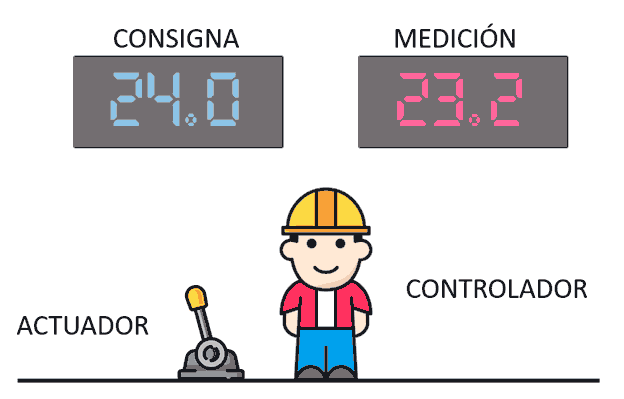
Lo único que sabes es que la palanca controla la potencia del sistema de climatización de un edificio. El número rojo es la temperatura real del edificio, y azul la que deseamos que sea. Tu misión, lógicamente, es que la temperatura real del edificio sea igual a la consigna.
Más allá de eso no sabes nada. No sabes cómo es el edificio, cómo es tu sistema de climatización, si han abierto todas las ventanas, si entran 100 personas en el edificio, si está amaneciendo, si es invierno. Ni siquiera sabes si al mover la palanca causas un efecto pequeño, o si vas a calcinar a alguien.
Como punto positivo, tenemos una entrada y salida continua (o semi continua), que es una necesidad para un control PID. Como vimos en la anterior, si el sensor o el actuador fueran de tipo on/off tendríamos que ir a un controlador todo/nada o controlador con histéresis.
Como hemos dicho, el controlador PID se basa en tres componentes, PID. Su “fortaleza” reside en el papel que cada uno de estos componentes tiene en la respuesta. A modo resumen, para que lo tengáis en la cabeza.
- El componente proporcional reacciona al presente
- El componente integral reacciona al pasado, y aporta “memoria” al controlador.
- El componente derivado reacciona al futuro, y aporta “predicción” al controlador
A continuación, vamos a entrar en profundidad en cada uno de los componentes, viendo su motivación, funcionamiento, y comportamiento.
Simulación de un PID
Para que podáis comprobar el comportamiento de los componentes del PID, tenemos esta simulación donde podéis ajustar los valores de Kp, Ki y Kd para visualizar la influencia de cada parámetro en la salida, y en la acción pedida por el controlador. z
Mueve los Slider de Kp, Ki y Kd para ver los cambios en la respuesta del controlador.
Componentes del PID
Para ello usaremos nuestro sencillo ejemplo de que te has despertado en mitad de una sala de control, sin saber nada más. Salvo que digamos lo contrario, la consigna (pantalla azul) está siempre a 24ºC.
Motivación
La motivación del componente proporcional seguramente sea el más intuitivo de explicar. Si entras en la habitación y ves 12ºC, parece lógico que tienes que darle más a la palanca que si pone 23ºC. ¿No?
Pues esa es la motivación del componente proporcional, que tiene sentido que apliques más acción cuanto más lejos estás del valor deseado, y viceversa.
Formulación
El componente proporcional se calcula simplemente como un factor K multiplicado por el error (diferencia entre consigna y valor real).
Comportamiento
El factor proporcional tiene una gran influencia en la velocidad de respuesta del sistema. Si tenemos una K pequeña, el sistema va a tardar mucho en alcanzar la consigna, porque le estamos dando “poca chicha” al actuador. Si lo aumentamos, conseguimos disminuir el tiempo de respuesta.
Pero si aumentamos la K demasiado podemos sobrepasar la consigna, oscilar, o incluso oscilar y mandarlo todo al garete. Vamos a ver cómo pasa eso.
Si tienes una K demasiado grande, le vas a dar demasiado a la palanca. Así al ver 18ºC, le das a la palanca y el siguiente valor es 25. Te has pasado. Bajas palanca, 21, ahora te has pasado hacia abajo. Subes palanca, 23. Bien, ya lo tienes.
Pero si llevas una K aún más grande, podría pasar que al ver 18º le des MUCHO a la palanca, y lo siguiente que verías podría ser 32ºC. ¡Ostras, me he pasado una barbaridad, BAJA LA PALANCA! 14º ¡OSTRAS SUBE SUBE! 45º… 8º… 56º… Acabas de hacer que tu sistema oscile y sea inestable (muerte, destrucción…).
Otra característica es que, en general, el componente proporcional no elimina por completo el error a largo plazo. En nuestro ejemplo, supongamos que a 22ºC y una posición de la palanca determinada, la energía que aportamos al edificio es la exactamente la que necesita el edificio para mantener la temperatura. Habríamos conseguido que la temperatura sea estable, pero como la posición de la palanca viene dada por el error (que se ha estabilizado) nunca podremos subir los 2ºC que nos faltan.
Motivación
La función del componente integral quizás sea el más complicado de explicar dentro del PID. Imaginar que estáis en la sala, y tenemos los 22ºC que teníamos antes. El proporcional te dice que pongas la pantalla en una posición y tú lo pones ahí. Pasa un minuto, pasa otro, pasa otro… y eso sigue en 22ºC, 2ºC por debajo de los que queremos.
El componente integral es el que dice… ¿oye chicos, igual hay que subir un poco la palanquita no? Porque llevamos un buen rato en 22ºC sin mover la palanca, y eso no tiene pinta de que vaya a irse. Pues esa voz con tanto sentido, que reacciona a la memoria del error pasado, es el componente integral.
Formulación
El componente integral aplica una acción que es proporcional a la integral del error a lo largo del tiempo. Equivalentemente, responde proporcionalmente a la suma de todos los errores anteriores.
Gráficamente corresponde con el área encerrado bajo la curva del error, que también es lo mismo que el área entre la salida y la consigna. En el campo discreto, la integral se sustituye por un método discreto para su cálculo, como el cálculo mediante rectángulos o trapecios.
Comportamiento
El componente integral permite al controlador eliminar por completo el error a largo plazo. Sin embargo, si Ki es muy pequeño, el sistema tardará mucho en eliminar el error.
Por otro lado, tened en cuenta que el término integral únicamente responde al área entre la salida y la consigna. Una consecuencia de ello es que si hemos acumulado (por ejemplo) un error por estar por debajo de la consigna, la única forma que tiene el término integral de compensarlo es estar un tiempo por encima.
Y efectivamente, el componente integral tiene tendencia a sobrepasar y oscilar, más incluso que el término proporcional.
Motivación
El componente derivado también es sencillo de explicar. Pongamos que estas tranquilamente con la temperatura a la consigna a 24ºC. ¡Todo perfecto! La temperatura baja a 23ºC, luego a 22ºC, y tu subes un poquito la palanca. Todo bien, muy tranquila la cosa.
Ahora imaginemos que, cuando estabas a 24ºC la temperatura baja a 18ºC de golpe. Ostras, eso es una buena bajada. Tu subes la palanca. Marca 12ºC … No sé si han abierto una ventana o qué está pasando, pero ¡esto está bajando muy rápido! Siguiente valor 2ºC ¡DALE DALE DALE, que se nos va de madre por segundos!
Esa es la función del componente derivado, reaccionar ante variaciones del error (por cambio de consigna o de la variable). Porque no es lo es lo mismo estar a 12ºC y subiendo lentamente, que si la temperatura se está desplomando a toda velocidad. Es decir, el termino derivado responde a la velocidad de cambio del error.
Formulación
El componente derivado se calcula de forma proporcional a la derivada del error respecto del tiempo en el momento presente. Equivalentemente, responde proporcionalmente a la diferencia entre el error actual y el error en el instante anterior.
En el campo discreto, la derivada se sustituye por la diferencia entre el error actual y el error anterior, dividido por el tiempo de muestreo (o se obvia esta división por completo y se incluye en el coeficiente Kd, si el tiempo de muestreo es constante).
Comportamiento
El componente derivado mejora la respuesta general de muchos sistemas para valores de Kd moderados. Sin embargo, si nos pasamos de Kd veremos que aparece una falta de “suavidad” en la respuesta, y otros comportamientos “raros”.
Además, el componente derivado responde muy mal al ruido de la medición. El ruido, una variación de alta frecuencia, supone variaciones muy rápidas, aunque sean de pequeña amplitud. Estas variaciones son amplificadas por el componente derivado.
Y, por último, el componente derivado a veces es un poco “bestia” porque pide acciones muy grandes. Imaginar, por ejemplo, un cambio instantáneo en la consigna. El componente derivado demandaría una acción infinita que, o el accionador no podría satisfacer. Como el accionador no podría dar la acción que solicita el controlador, tendríamos desviaciones respecto a lo calculado, o incluso podríamos dañar el accionador.
Conclusión
Hemos visto el control PID, uno de los controladores PID más empleados y versátiles que pueden controlar una gran variedad de sistemas con buenos resultados, sin necesidad de caracterizar la planta.
El comportamiento del PID se basa en la suma de sus tres componentes, que se controlan a través de las constantes Kp, Ki y Kd. Las tres constantes tienen que ser calibradas para la planta a controlar, y de este ajuste depende que la respuesta del sistema sea buena, mala, o muy muy mala.
Al proceso de ajuste de las constantes se le denomina “tunning” de un control PID, y en la próxima entrada de la serie veremos distintas estrategias para ajustar el PID. ¡Hasta pronto!