Today we are going to talk about Gamma correction, a fundamental aspect to consider when working with light sources in which we want to vary the intensity using a processor like Arduino.
Let’s consider the simple case of an LED in which we want to vary the brightness. Very easy, right? We simply use a PWM signal to turn the LED on and off as we saw in the last example of this post.
With this, we are turning off the LED for a certain percentage of the time, so fast that we can’t see it. The brightness, as expected, should vary in the same ratio as the time the LED is turned off (spoiler, it’s not going to be that way).
If you do this very simple experiment, turning on the LED according to a triangular function, you will see that the response of the LED is not at all linear. In fact, your LED will be “practically on” most of the time, and the decrease and increase in brightness will occur in a very short period of time.
How can this be? What is happening here? Ah, my friend… this is where Gamma correction comes in.
Gamma correction
What is happening is that your eye-brain is deceiving you. Your visual perception system is designed to work in a high range and to be especially sensitive to changes in low light.
Even assuming that your emitter’s response is linear (which, in many cases, we can assume to be true) it is your perception of light that is not linear with respect to the amount of light it perceives.
That is, when your “eye-brain” sees an LED lit at 50% (half on or half off, depending on how optimistic you are) your perception is not “it’s shining at 50%”.
The human visual perception follows an approximately potential form. Something similar to the orange curve in the following graph.
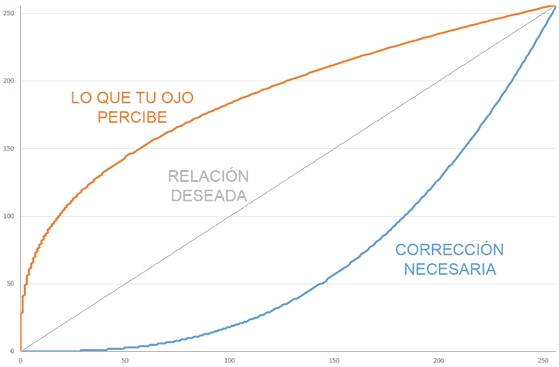
In order for the perception to match the desired value (grey curve, completely linear), we need to apply a correction to the values we apply to the light source.
This correction is what we call Gamma correction and is represented in the previous graph by the blue curve.
Too weird? Well, that’s how your brain works.
A numerical example
In case it still seems too weird to you and to show how important the effect of gamma correction is, let’s try to illustrate it with a small numerical example.
Suppose you want to turn on an LED at 30% brightness by applying a PWM between 0 and 255. The “logical” thing would be to apply a value of 0.3 * 255 to the PWM, that is, around 77.
But, if we look at the perception curve (orange) with a value of 77, you would perceive a brightness around 65%. More than double what you expected!
To obtain a relationship really around 30% brightness, you should apply a value of 8 (yes, only 8 out of 255). As you can see, the difference between applying gamma correction or not is enormous.
This becomes even more important when working with RGB lights or LED strips. If we do not take gamma correction into account, the color obtained will be completely different from what we intended to obtain.
Applying Gamma correction in Arduino
Fortunately, applying Gamma correction in a processor like Arduino is very simple. Simply we must correct the value that we are going to send to the PWM (or to the controller we are using).
One way to do this is to use a table with the corrections that includes the gamma correction values needed for an 8-bit value.
const static uint8_t PROGMEM GammeTable8[] = {
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2,
2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5,
5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 10,
10, 10, 11, 11, 11, 12, 12, 13, 13, 13, 14, 14, 15, 15, 16, 16,
17, 17, 18, 18, 19, 19, 20, 20, 21, 21, 22, 22, 23, 24, 24, 25,
25, 26, 27, 27, 28, 29, 29, 30, 31, 32, 32, 33, 34, 35, 35, 36,
37, 38, 39, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 50,
51, 52, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 66, 67, 68,
69, 70, 72, 73, 74, 75, 77, 78, 79, 81, 82, 83, 85, 86, 87, 89,
90, 92, 93, 95, 96, 98, 99,101,102,104,105,107,109,110,112,114,
115,117,119,120,122,124,126,127,129,131,133,135,137,138,140,142,
144,146,148,150,152,154,156,158,160,162,164,167,169,171,173,175,
177,180,182,184,186,189,191,193,196,198,200,203,205,208,210,213,
215,218,220,223,225,228,231,233,236,239,241,244,247,249,252,255 };
uint8_t CorrectGamma_Table8(uint8_t value)
{
result = pgm_read_byte(&GammeTable8[value]);
}
Which in the code we would use to correct the values before sending to the emitter, for example, when writing the PWM or before sending it to the controller.
analogWrite(pin, CorrectGamma_Table8(PWM));
This table is stored in flash memory, occupying 256 bytes. Which is quite acceptable, and has the advantage that the correction calculation is very fast.
Another option is to use integer arithmetic to adjust an equation to the gamma relationship. We avoid using floating point numbers to avoid the calculation involved. Thus, we arrive at the following function.
uint8_t CorrectGamma8(uint8_t value)
{
return (((45 * ((unsigned long)value + 1) + 3488) * ((unsigned long)value + 1) - 136379) * ((unsigned long)value + 1) + 1305350) / 3722130;
}
Which, for example, we would use like this.
analogWrite(pin, CorrectGamma8(PWM));
The results obtained are similar to those obtained when using the table. This method has the advantage of occupying less memory although, on the other hand, it is slightly slower (but very little).
Gamma correction in a Library
What if we put it all in a library? Of course we can. Here is the CorrectionGamma library, an Open Source library for Arduino that has the two methods we have seen in this post to be able to use them comfortably and easily.