In this post we are going to see how to model a finite state machine in a processor like Arduino.
A finite state machine is a computational abstraction commonly used. It is a systematic way of programming an automaton. For this reason, they are widely used in the development of small and medium-sized projects.
Examples of what we can do with a state machine are, for example, vending machines, elevators, parking barriers, industrial stations, and even small robots, among many others.
What is a state machine?
A state machine models the behavior of an automatic machine. It is made up of states, transitions, inputs, and outputs.
State machines are often represented with diagrams, in which each state corresponds to a circle, and the transitions with arrows that connect them. Sometimes the inputs and outputs of the system are added according to different conventions.
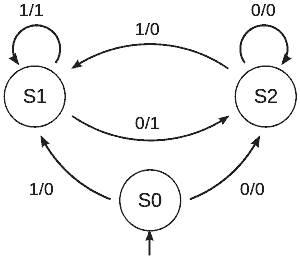
The states describe the possible combinations of the internal variables of the automaton at a given moment. An automaton starts from an initial state and, as events occur, changes to the different states that describe its possible behavior.
The changes from one state to another are determined by transitions, which have a certain condition associated with them. The conditions associated with state change transitions can depend on both external (inputs) and internal variables.
Finally, a state machine must perform actions (or outputs). These can be associated with the states (Moore machine) or the transitions (Mealy machine), both approaches being similar in their formulation.
Example of a state machine
We are going to make a simple implementation of a state machine in a processor like Arduino. The machine that we are going to implement as an example corresponds to the following scheme.
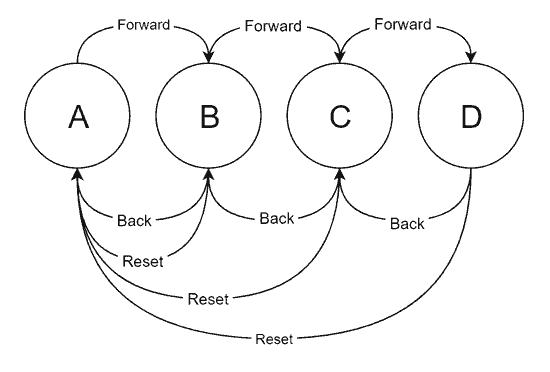
As we can see, it is a very simple machine that has 4 states A, B, C, and D. We have three possible inputs, Fordward, Backward, and Reset.
With Fordward and Backward the machine moves to the next and previous state. On the other hand, the Reset input causes the machine to return to state A, from any other state.
It has been decided that the states are not cyclical. That is, Forward does not go from D to A, nor Backward goes from A to D. Although we could have done it without much effort.
State machine in Arduino
A possible implementation of the state machine could be the following.
enum State
{
PosicionA,
PosicionB,
PosicionC,
PosicionD
};
enum Input
{
Unknown,
Reset,
Forward,
Backward
};
// Global variables
State currentState;
Input currentInput;
// State actions and transition conditions
void stateA()
{
if (currentInput == Input::Forward)
changeState(State::PosicionB);
}
void stateB()
{
if (currentInput == Input::Backward)
changeState(State::PosicionA);
if (currentInput == Input::Forward)
changeState(State::PosicionC);
if (currentInput == Input::Reset)
changeState(State::PosicionA);
}
void stateC()
{
if (currentInput == Input::Backward)
changeState(State::PosicionB);
if (currentInput == Input::Forward)
changeState(State::PosicionD);
if (currentInput == Input::Reset)
changeState(State::PosicionA);
}
void stateD()
{
if (currentInput == Input::Backward)
changeState(State::PosicionC);
if (currentInput == Input::Reset)
changeState(State::PosicionA);
}
// Outputs associated with transitions
void outputA()
{
Serial.println("A B C D");
Serial.println("X ");
Serial.println();
}
void outputB()
{
Serial.println("A B C D");
Serial.println(" X ");
Serial.println();
}
void outputC()
{
Serial.println("A B C D");
Serial.println(" X ");
Serial.println();
}
void outputD()
{
Serial.println("A B C D");
Serial.println(" X");
Serial.println();
}
void setup()
{
Serial.begin(9600);
currentState = PosicionA;
outputA();
}
void loop()
{
readInput();
updateStateMachine();
}
// Updates the state of the machine
void updateStateMachine()
{
switch (currentState)
{
case PosicionA: stateA(); break;
case PosicionB: stateB(); break;
case PosicionC: stateC(); break;
case PosicionD: stateD(); break;
}
}
// Reads the input from the serial port
void readInput()
{
currentInput = Input::Unknown;
if (Serial.available())
{
char incomingChar = Serial.read();
switch (incomingChar)
{
case 'R': currentInput = Input::Reset; break;
case 'A': currentInput = Input::Backward; break;
case 'D': currentInput = Input::Forward; break;
default: break;
}
}
}
// Function that changes the state and triggers the transitions
void changeState(int newState)
{
currentState = newState;
switch (currentState)
{
case State::PosicionA: outputA(); break;
case State::PosicionB: outputB(); break;
case State::PosicionC: outputC(); break;
case State::PosicionD: outputD(); break;
default: break;
}
}As we can see, first, we have defined two enumerations that correspond to the possible states and inputs. It is a good practice to simplify the readability of the code, its maintainability, and scalability.
On the other hand, we have 2 global variables currentState and currentInput, which store the current state of the state machine, and the last received input.
Next, we have a function (state) for each of the states. These actions contain the logic associated with the transitions, i.e., they make the change to another state based on a condition. In this case, the only conditions we have are the input variables, but they could be timeouts, or anything else.
On the other hand, we have the output functions (output) of each state, which are triggered when entering a node. In this example, we only show a representation through the serial port of the state of the machine. In a real machine, we would perform the necessary actions.
To switch between states we use the function changeState(int newState), which checks the current state with the new state. Here we launch the input functions in each state.
If we wanted to associate a function with a particular transition, instead of entering a state we could, for example, launch them in the state functions when making the state change.
Finally, the machine is constantly updated through the Update() function. This function only launches the corresponding state function for the current state, and with this it manages to update the state of the machine.
In the example, we also have the readInput() function, which receives a character from the serial port. A, D, and R correspond, respectively, to the Backward, Fordward, and Reset inputs. This function is not properly of the state machine, we just use it in the example to check the operation.
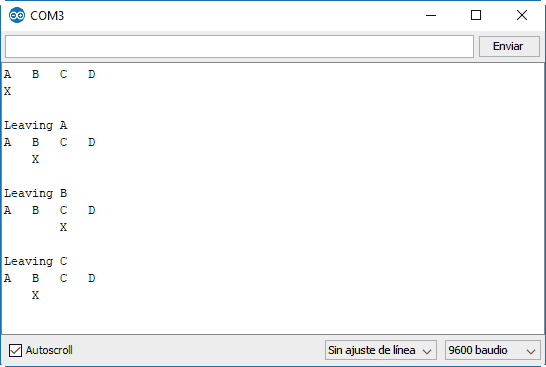
Results
If we run the above code we can see the result on the serial port. We can change the state by pressing the ‘A’, ‘D’, and ‘R’ keys.
Tabular state machine in Arduino
Next, we will see a variation of the previous code, a tabular implementation of a state machine.
The main differences are that in this case the transitions between states are collected in a state transition matrix, instead of in the previous functions for each state. The new state is obtained by the combined index of the current state and input.
Similarly, the actions associated with the transitions are collected in a vector of functions, so that we can access each one directly by the index of the current state.
enum State
{
PosicionA,
PosicionB,
PosicionC,
PosicionD
};
enum Input
{
Unknown,
Reset,
Forward,
Backward
};
const void outputA()
{
Serial.println("A B C D");
Serial.println("X ");
Serial.println();
}
const void outputB()
{
Serial.println("A B C D");
Serial.println(" X ");
Serial.println();
}
const void outputC()
{
Serial.println("A B C D");
Serial.println(" X ");
Serial.println();
}
const void outputD()
{
Serial.println("A B C D");
Serial.println(" X");
Serial.println();
}
typedef void (*const StateFunc)();
State currentState;
Input currentInput;
const StateFunc transitionOutput[] PROGMEM = { outputA, outputB, outputC, outputD};
const byte stateChange[4][4] PROGMEM =
{
{ PosicionA, PosicionA, PosicionB, PosicionA },
{ PosicionB, PosicionA, PosicionC, PosicionA },
{ PosicionC, PosicionA, PosicionD, PosicionB },
{ PosicionD, PosicionA, PosicionD, PosicionC },
};
void setup()
{
Serial.begin(9600);
currentState = PosicionA;
outputA();
}
void loop()
{
readInput();
updateStateMachine();
}
void updateStateMachine()
{
State newState = (State)pgm_read_byte(&stateChange[currentState][currentInput]);
if (currentState == newState) return;
currentState = newState;
StateFunc pStateFunc = (StateFunc)pgm_read_ptr(&transitionOutput[currentState]);
pStateFunc();
}
void readInput()
{
currentInput = Input::Unknown;
if (Serial.available())
{
char incomingChar = Serial.read();
switch (incomingChar)
{
case 'R': currentInput = Input::Reset; break;
case 'A': currentInput = Input::Backward; break;
case 'D': currentInput = Input::Forward; break;
default: break;
}
}
}The tabular implementation has advantages in certain cases. The execution of the code is slightly more efficient, since, instead of computing conditionals for state transitions and associated actions, we access directly through the indices of the matrix.
In addition, in certain cases it can be slightly more efficient in the use of memory, since the transitions can be directly mapped into program memory (ROM), instead of in dynamic memory (RAM).
Finally, it is easier to change the behavior of the network, simply by altering the transition matrix. This change can, for example, be updated from an SD card, or received by a means of communication (UART, Bluetooth, Wifi…).
However, it is considerably more restrictive. Any input to the machine has to be mapped to an input, which makes it counterproductive in the (very common) case of having transitions with combined conditions (for example, in the case of condition A&B, we would have to create a new input), timeouts, etc…
In any case, it was not possible to make an entry on finite state machines without presenting a tabular approach to the problem. So here it is as an alternative, with its respective advantages and disadvantages.
State machine in a library
Finally, the most useful and convenient option is to encapsulate the finite state machine in an object. Here we have the StateMachine library that allows implementing state machines on a processor like Arduino.
With this library, the code for this example would look like this.
#include "StateMachineLib.h"
enum State
{
PosicionA = 0,
PosicionB = 1,
PosicionC = 2,
PosicionD = 3
};
enum Input
{
Reset = 0,
Forward = 1,
Backward = 2,
Unknown = 3,
};
StateMachine stateMachine(4, 9);
Input input;
void setupStateMachine()
{
stateMachine.AddTransition(PosicionA, PosicionB, []() { return input == Forward; });
stateMachine.AddTransition(PosicionB, PosicionA, []() { return input == Backward; });
stateMachine.AddTransition(PosicionB, PosicionC, []() { return input == Forward; });
stateMachine.AddTransition(PosicionB, PosicionA, []() { return input == Reset; });
stateMachine.AddTransition(PosicionC, PosicionB, []() { return input == Backward; });
stateMachine.AddTransition(PosicionC, PosicionD, []() { return input == Forward; });
stateMachine.AddTransition(PosicionC, PosicionA, []() { return input == Reset; });
stateMachine.AddTransition(PosicionD, PosicionC, []() { return input == Backward; });
stateMachine.AddTransition(PosicionD, PosicionA, []() { return input == Reset; });
stateMachine.SetOnEntering(PosicionA, outputA);
stateMachine.SetOnEntering(PosicionB, outputB);
stateMachine.SetOnEntering(PosicionC, outputC);
stateMachine.SetOnEntering(PosicionD, outputD);
stateMachine.SetOnLeaving(PosicionA, []() {Serial.println("Leaving A"); });
stateMachine.SetOnLeaving(PosicionB, []() {Serial.println("Leaving B"); });
stateMachine.SetOnLeaving(PosicionC, []() {Serial.println("Leaving C"); });
stateMachine.SetOnLeaving(PosicionD, []() {Serial.println("Leaving D"); });
}
void setup()
{
Serial.begin(9600);
Serial.println("Starting State Machine...");
setupStateMachine();
Serial.println("Start Machine Started");
stateMachine.SetState(PosicionA, false, true);
}
void loop()
{
input = static_cast<Input>(readInput());
stateMachine.Update();
}
int readInput()
{
Input currentInput = Input::Unknown;
if (Serial.available())
{
char incomingChar = Serial.read();
switch (incomingChar)
{
case 'R': currentInput = Input::Reset; break;
case 'A': currentInput = Input::Backward; break;
case 'D': currentInput = Input::Forward; break;
default: break;
}
}
return currentInput;
}
void outputA()
{
Serial.println("A B C D");
Serial.println("X ");
Serial.println();
}
void outputB()
{
Serial.println("A B C D");
Serial.println(" X ");
Serial.println();
}
void outputC()
{
Serial.println("A B C D");
Serial.println(" X ");
Serial.println();
}
void outputD()
{
Serial.println("A B C D");
Serial.println(" X");
Serial.println();
}The advantage of having the logic in a class is that it is much more convenient to use, the code is cleaner and more compact, and it is easier to maintain and scale.
The disadvantage is that we will have a slight performance penalty. In most cases, this will be of no importance and is perfectly acceptable, compared to the advantage of convenience and code.
Download the code
All the code in this post is available for download on Github.