We continue with digital filters as a way to improve the values obtained in sensor measurements in our electronics and robotics projects with Arduino.
So far we have seen the moving average filter and the EMA exponential filter for low-pass and high-pass filtering and double EMA for band-pass and stop-band filtering. These filters are simple and efficient to implement but have the disadvantage of being not very robust/stable in the presence of spurious points (points that deviate significantly from the real value).
This is because both filters (moving average and exponential filter) are based on the mean as an estimator of trend. As we saw when discussing fast median calculation in Arduino, the mean is a not very robust trend estimator. Its popularity is largely due to its simplicity of calculation and the fact that it is a function that we can manipulate and derive.
The best example to illustrate the instability of the mean is its behavior in the presence of spurious points. A single anomalous point can cause a large deviation in the mean, ruining a whole series of measurements, showing the lack of robustness of the mean as an estimator of trend.
Fortunately, the mean is not the only trend estimator. Here statistics comes to the rescue, specifically the branch of robust statistics, which is responsible for making calculations more stable than traditional statistics. And precisely robust statistics uses the median as an indicator of trend.
In this post we will focus on implementing a moving median filter efficiently, and light enough to fit in a microprocessor like Arduino.
The moving median filter
Similar to the moving average filter, the moving median filter defines a window of N elements, which collects the last N measurements. The value of the filter is the median of the values contained in the window.
Increasing the size of the window increases the smoothing of the signal but adds a delay to the signal (as was the case with the moving average and EMA filter) since it is necessary to “wait” for the sampling of more points.
The size of the window will depend on the characteristics of our system and the signal to be filtered, but window sizes of 5 to 11 are common. In general, odd window sizes are preferred to avoid having to average between two samples, which would eliminate part of the filtering capacity of the median.
A moving median filter is a very useful and widely used instrument in electronics. They are widely used in data acquisition systems and sensor detection for noise elimination, for example, in gyroscopes and accelerometers.
The moving median filter has better characteristics in filtering certain types of signals, especially those that have spurious signals or salt and pepper noise (noise that causes points to go to the minimum or maximum possible).
On the other hand, using the median as a filter also has its disadvantages. The most obvious is that, in general, it is a more computationally expensive calculation. It is usually considered that the calculation of the median involves ordering all the values contained, which we showed is not true when discussing the calculation of the median.
On the other hand, the median filter can only return sampled points, so we lose the ability to “interpolate” (subsample) that we can obtain with other filters. This causes the filtered signals to be “angular” and present discrete jumps.
However, it is possible to improve the behavior by combining the moving median filter with an exponential EMA filter, taking into account that the factor of both filters will accumulate. Therefore, we must reach a compromise, reducing the size of the window and the alpha of the EMA to avoid increasing the overall delay.
Moving median filter results
To illustrate the behavior of the moving median filter, we will show the results for the same simulated input signal and different window sizes.
The first figure shows the median filter for a window size of 3. We see that it has removed most of the “peaks” in the signal, which corresponds to what we have commented on the capacity of the median filter for the elimination of spurious signals and noise.
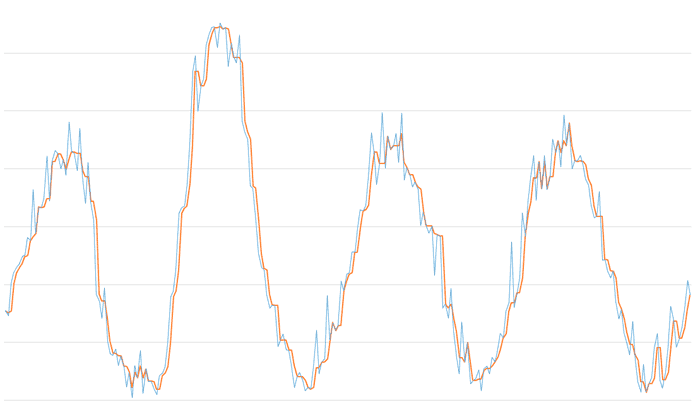
However, a window size of 3 is usually insufficient, as if two anomalous points coincide, the filter would only be able to absorb/eliminate one.
The next graph shows the result for a window of size 5. With a larger window, the median filter increases its strength against noise. However, we see the angular and “jumpy” behavior we mentioned before.
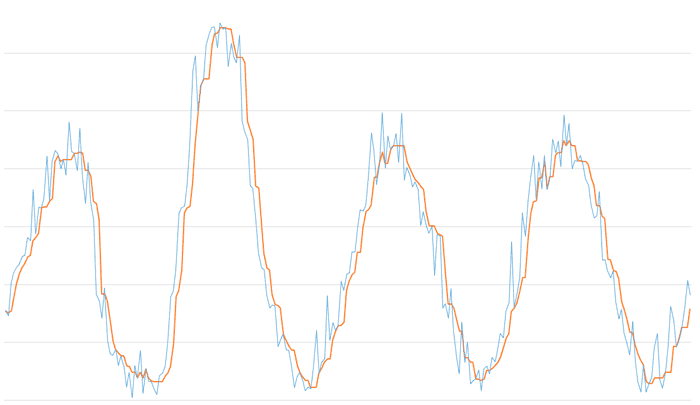
The next graph shows the result for a window size of 11. The filtered signal increases its smoothness, but the delay starts to become evident.
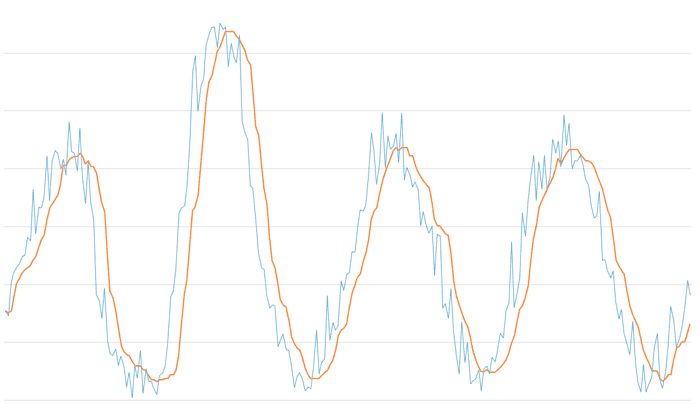
Finally, the last graph shows the combination of a median filter with a window size of 3 with an exponential EMA filter with Alpha 0.3
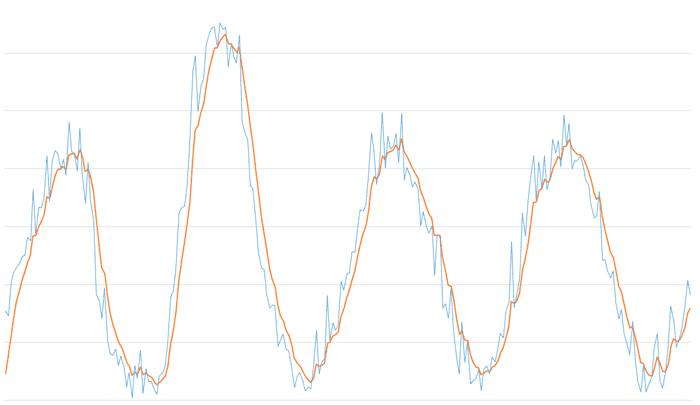
We see that the combination of a median filter with a reduced window (5 would be a good value) together with an EMA with moderate alpha provides the noise and spurious signal filtering of the median along with the smoothness and subsampling provided by the EMA, while maintaining the delay at acceptable values.
Implementing a median filter on Arduino
Let’s try three different implementations for the implementation of a moving median filter. I will tell you in advance (spoiler!) that the most efficient one is logically going to be the last one. But we will present the three, especially for those stubbornly implementing the median filter with a simple sorting algorithm :).
Median filter with Quick Sort
The first option is to sort the values in the window with a sorting algorithm. In the post on sorting with QuickSort we already demonstrated that it is much faster than other alternatives such as the famous (and inefficient) bubble sort method or the slightly less famous (and not much less famous) insertion method.
Therefore, we will only test our Quick Sort algorithm. A lightweight implementation of the median filter with Quick Sort would be as follows.
const int windowSize = 3;
int buffer[windowSize];
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
#define MEDIAN(a, n) a[(((n)&1)?((n)/2):(((n)/2)-1))];
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
int elementCount;
float AddValue(int value)
{
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
memcpy(buffer, medianBuffer, sizeof(medianBuffer));
QuickSortAsc(buffer, 0, elementCount - 1);
int med = MEDIAN(medianBuffer, windowSize);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
void QuickSortAsc(int* arr, const int left, const int right)
{
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
while (i <= j)
{
while (arr[i]<pivot) i++;
while (arr[j]>pivot) j--;
if (i <= j)
{
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
if (left<j)
QuickSortAsc(arr, left, j);
if (i<right)
QuickSortAsc(arr, i, right);
}
Median filter with Quick Median
The next evolution is that, as we saw in the post on calculating the median quickly on Arduino, there are more efficient algorithms to calculate the median that do not require complete sorting of the vector.
In the post we tested different algorithms, finally opting for the Quick Select algorithm modified by Wirth for its high efficiency and relatively simple implementation, suitable for a processor like Arduino.
Therefore, we are going to try to implement the median filter using the Quick Select Wirth algorithm for calculating the median of the window. One disadvantage of the method is that the Quick Select algorithm modifies the vector, so we will have to copy the window to an intermediate buffer for the calculation.
The implementation would be as follows.
const int windowSize = 33;
int buffer[windowSize];
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
#define ELEM_SWAP(a,b) { int t=(a);(a)=(b);(b)=t; }
#define MEDIAN(a,n) kth_smallest(a,n,(((n)&1)?((n)/2):(((n)/2)-1)))
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
int elementCount;
float AddValue(int value)
{
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
memcpy(buffer, medianBuffer, sizeof(medianBuffer));
int med = MEDIAN(medianBuffer, elementCount);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
int kth_smallest(int a[], int n, int k)
{
int i, j, l, m;
int x;
l = 0;
m = n - 1;
while (l<m)
{
x = a[k];
i = l;
j = m;
do {
while (a[i]<x) i++;
while (x<a[j]) j--;
if (i <= j)
{
ELEM_SWAP(a[i], a[j]);
i++;
j--;
}
} while (i <= j);
if (j<k) l = i;
if (k<i) m = j;
}
return a[k];
}
Quick Median Filter Median Filter
The last algorithm tested is the algorithm proposed by Phil Ekstrom in November 2000. Ekstrom uses a combination of circular buffer and linked list to improve the efficiency of the median filter, especially for large window sizes.
Similar to the motivation for using a circular buffer to calculate the moving average filter, Ekstrom’s algorithm finds its origin in the fact that adding a new value and removing the oldest one from the window does not substantially modify its structure. In particular, it is not necessary to process it completely.
Ekstrom uses a circular buffer to store the window elements according to their age. On the other hand, each element contains a pointer to the next smaller element, forming a linked list.
Adding a new element to the circular buffer and inserting an element in the linked list is immediate. The only real computational cost is finding the insertion point, for which it is necessary to traverse the linked list.
The implementation is simple and suitable for a microprocessor like Arduino. However, it is possible to improve its efficiency, just as there are algorithms with better efficiency, at the cost of greater memory usage.
#define MEDIAN_FILTER_WINDOW 7
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
int med = medianFilter(value);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(values[iCount]);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
#define STOPPER 0
uint16_t medianFilter(uint16_t value)
{
struct node
{
struct node *next;
uint16_t value;
};
static struct node buffer[MEDIAN_FILTER_WINDOW] = { 0 };
static struct node *iterator = buffer;
static struct node smaller = { nullptr, STOPPER };
static struct node bigger = { &smaller, 0 };
struct node *successor;
struct node *accessor;
struct node *accessorPrev;
struct node *median;
uint16_t i;
if (value == STOPPER)
value++;
if ((++iterator - buffer) >= MEDIAN_FILTER_WINDOW)
iterator = buffer;
iterator->value = value;
successor = iterator->next;
median = &bigger;
accessorPrev = nullptr;
accessor = &bigger;
if (accessor->next == iterator)
accessor->next = successor;
accessorPrev = accessor;
accessor = accessor->next;
for (i = 0; i < MEDIAN_FILTER_WINDOW; ++i)
{
if (accessor->next == iterator)
accessor->next = successor;
if (accessor->value < value)
{
iterator->next = accessorPrev->next;
accessorPrev->next = iterator;
value = STOPPER;
};
median = median->next;
if (accessor == &smaller)
break;
accessorPrev = accessor;
accessor = accessor->next;
if (accessor->next == iterator)
accessor->next = successor;
if (accessor->value < value)
{
iterator->next = accessorPrev->next;
accessorPrev->next = iterator;
value = STOPPER;
}
if (accessor == &smaller)
break;
accessorPrev = accessor;
accessor = accessor->next;
}
return median->value;
}
Bonus: 3-size median filter
If we are using a window size 3, the filter allows for a much simpler and more efficient implementation.
const int windowSize = 3;
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
float AddValue(int value)
{
appendToBuffer(value);
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
int med = median3(medianBuffer);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
int median3(int arr[])
{
if ((arr[0] <= arr[1]) && (arr[0] <= arr[2]))
return (arr[1] <= arr[2]) ? arr[1] : arr[2];
else if ((arr[1] <= arr[0]) && (arr[1] <= arr[2]))
return (arr[0] <= arr[2]) ? arr[0] : arr[2];
else
return (arr[0] <= arr[1]) ? arr[0] : arr[1];
}
Comparison
Here is the time required to execute the different algorithms, for different window sizes. All of them have been performed on an Arduino Nano 16Mhz. The results are shown in us.
| Window | QuickSort | Wirth | Ekstrom | Direct |
|---|---|---|---|---|
| 3 | 23.28 | 23.02 | 14.14 | 5.29 |
| 5 | 44.03 | 32.67 | 18.02 | - |
| 7 | 64.83 | 42.37 | 22.37 | - |
| 9 | 94.34 | 53.15 | 26.83 | - |
| 11 | 115.94 | 64.86 | 30.83 | - |
| 33 | 403.73 | 189.25 | 80.78 | - |
As we can see, the Ekstrom algorithm is much faster than the rest of the alternatives, even having used very fast algorithms for sorting (Quick Sort) and calculating the median (Quick Select Wirth).
Logically, for a window size of 3, the direct algorithm is much faster, but we normally won’t use a size of 3 because, as we have mentioned, it is too small.
For common values of (from 5 to 11) the median filter with the Ekstrom algorithm is about 2 times faster than the median calculation with Quick Select, and 3 times faster than sorting with Quick Select. Larger window sizes provide even greater advantages in favor of Ekstrom.
Fast median filter in a library
What if we clean up and improve the code, and put it into a library to make it more convenient to use? Of course, yes, here is a Median Filter library for Arduino. Enjoy it!
Download the code
All the code in this post is available for download on Github.