Sorting vectors is a frequent need in computer science and a task that, in general, can consume large amounts of memory and processor time.
For this reason, choosing an efficient sorting algorithm is an important need to improve the speed of our programs.
In this post we are going to implement the Bubble Sort algorithm to sort a vector in ascending and descending order.
The Bubble Sort algorithm is one of the simplest and best-known methods for sorting a vector. It is often used as an example in programming courses, which is why its implementation is very common.
However, Bubble Sort is an inefficient algorithm that involves traversing the N-sized sample of size N. This translates to an order of complexity of O(n^2), making it impractical except for samples with a very small number of elements.
In the next post, we will implement the QuickSort algorithm, a much more efficient sorting algorithm, and compare the results with those obtained using Bubble Sort.
For the Bubble Sort test, we will try two samples with unordered numbers from 1 to 100 and 1 to 500, on an Arduino Nano with 16Mhz.
Of course, Arduino is not the most suitable machine for sorting such a large number of elements due to its power and memory limitations. If we really need to sort very large collections, we are probably not using the right processor. But we are not going to test the algorithms with 10 elements, are we?
Below is the implementation of the Bubble Sort algorithm in ascending and descending order.
int values100[] = { 3, 53, 70, 56, 18, 85, 27, 14, 37, 94, 9, 55, 40, 60, 52, 61, 15, 65, 13, 8, 57, 97, 69, 4, 35, 82, 22, 73, 59, 68, 78, 24, 21, 36, 71, 80, 74, 39, 17, 12, 29, 76, 49, 51, 30, 90, 88, 2, 84, 50, 62, 28, 77, 43, 5, 16, 58, 26, 32, 34, 1, 75, 66, 95, 38, 89, 67, 87, 100, 54, 92, 81, 25, 83, 46, 33, 23, 45, 96, 99, 79, 48, 11, 31, 7, 6, 19, 91, 93, 44, 47, 98, 86, 41, 63, 20, 72, 10, 42, 64 };
int values100Length = sizeof(values100) / sizeof(int);
int values500[] = { 404, 267, 446, 214, 45, 149, 475, 496, 233, 78, 248, 307, 95, 431, 479, 445, 181, 370, 458, 476, 371, 122, 231, 74, 8, 392, 355, 397, 426, 125, 15, 159, 172, 369, 441, 318, 203, 399, 249, 225, 457, 351, 462, 184, 384, 100, 265, 244, 32, 499, 448, 29, 412, 447, 110, 473, 12, 414, 311, 301, 56, 84, 243, 378, 210, 217, 165, 10, 79, 374, 337, 52, 373, 395, 30, 126, 116, 280, 313, 474, 157, 6, 467, 459, 381, 129, 482, 13, 179, 167, 72, 68, 112, 194, 205, 97, 342, 142, 4, 418, 22, 440, 430, 364, 82, 483, 158, 198, 124, 259, 20, 312, 241, 254, 456, 361, 5, 245, 281, 376, 461, 274, 219, 348, 235, 23, 328, 2, 136, 291, 455, 302, 107, 415, 393, 43, 427, 211, 223, 168, 340, 87, 286, 133, 228, 354, 182, 204, 67, 419, 63, 270, 463, 60, 49, 358, 362, 102, 330, 242, 406, 108, 221, 83, 300, 363, 166, 290, 389, 436, 263, 34, 487, 377, 106, 491, 434, 257, 207, 417, 47, 379, 343, 500, 339, 403, 390, 61, 495, 262, 128, 132, 293, 94, 69, 143, 279, 375, 421, 109, 237, 310, 432, 218, 161, 150, 470, 200, 121, 464, 494, 443, 466, 252, 33, 105, 173, 344, 275, 388, 289, 333, 409, 452, 118, 315, 489, 283, 433, 442, 439, 114, 334, 229, 304, 175, 253, 216, 236, 256, 70, 169, 321, 365, 405, 366, 91, 380, 37, 212, 429, 336, 141, 308, 90, 492, 31, 460, 324, 387, 156, 120, 24, 183, 401, 81, 51, 288, 3, 367, 246, 498, 39, 386, 36, 192, 352, 292, 451, 294, 50, 326, 345, 76, 319, 360, 335, 306, 48, 239, 309, 468, 331, 226, 385, 347, 295, 44, 89, 497, 438, 332, 297, 346, 25, 199, 485, 469, 55, 402, 193, 284, 264, 135, 7, 14, 53, 197, 88, 201, 232, 258, 234, 481, 255, 9, 186, 59, 162, 18, 98, 93, 154, 73, 327, 278, 230, 131, 145, 26, 465, 103, 220, 19, 316, 177, 407, 146, 42, 153, 144, 99, 117, 28, 62, 148, 282, 453, 137, 208, 424, 450, 1, 477, 164, 368, 119, 21, 396, 127, 484, 277, 130, 437, 111, 206, 64, 391, 322, 151, 372, 188, 191, 57, 160, 383, 411, 180, 104, 16, 147, 170, 285, 350, 394, 71, 190, 54, 251, 261, 272, 320, 196, 338, 425, 227, 178, 420, 123, 174, 276, 480, 138, 80, 486, 454, 490, 435, 400, 77, 444, 323, 140, 171, 139, 195, 260, 314, 92, 17, 449, 222, 187, 296, 96, 40, 58, 423, 152, 11, 269, 359, 329, 422, 410, 155, 250, 101, 240, 213, 478, 273, 189, 27, 471, 356, 416, 238, 35, 41, 398, 113, 268, 46, 215, 85, 488, 325, 163, 202, 247, 341, 382, 299, 185, 176, 224, 472, 115, 349, 271, 303, 287, 408, 428, 65, 134, 75, 305, 66, 298, 357, 38, 266, 353, 209, 493, 317, 86, 413 };
int values500Length = sizeof(values500) / sizeof(int);
void printArray(int* x, int length)
{
for (int iCount = 0; iCount < length; iCount++)
{
Serial.print(x[iCount]);
Serial.print(',');
}
}
void setup()
{
Serial.begin(115200);
Serial.println("Sorting 100 values");
long timeCount = micros();
BubbleSortAsc(values100, values100Length);
timeCount = micros() - timeCount;
printArray(values100, values100Length);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
Serial.println("");
Serial.println("Sorting 500 values");
timeCount = micros();
BubbleSortAsc(values500, values500Length);
timeCount = micros() - timeCount;
printArray(values500, values500Length);
Serial.println();
Serial.print(timeCount);
Serial.println("us");
}
void loop()
{
}
void BubbleSortAsc(int* values, int length)
{
int i, j, flag = 1;
int temp;
for (i = 1; (i <= length) && flag; i++)
{
flag = 0;
for (j = 0; j < (length - 1); j++)
{
if (values[j + 1] < values[j])
{
temp = values[j];
values[j] = values[j + 1];
values[j + 1] = temp;
flag = 1;
}
}
}
}
void BubbleSortDesc(int* values, int length)
{
int i, j, flag = 1;
int temp;
for (i = 1; (i <= length) && flag; i++)
{
flag = 0;
for (j = 0; j < (length - 1); j++)
{
if (values[j + 1] > values[j])
{
temp = values[j];
values[j] = values[j + 1];
values[j + 1] = temp;
flag = 1;
}
}
}
}And the results we obtain when performing the benchmark.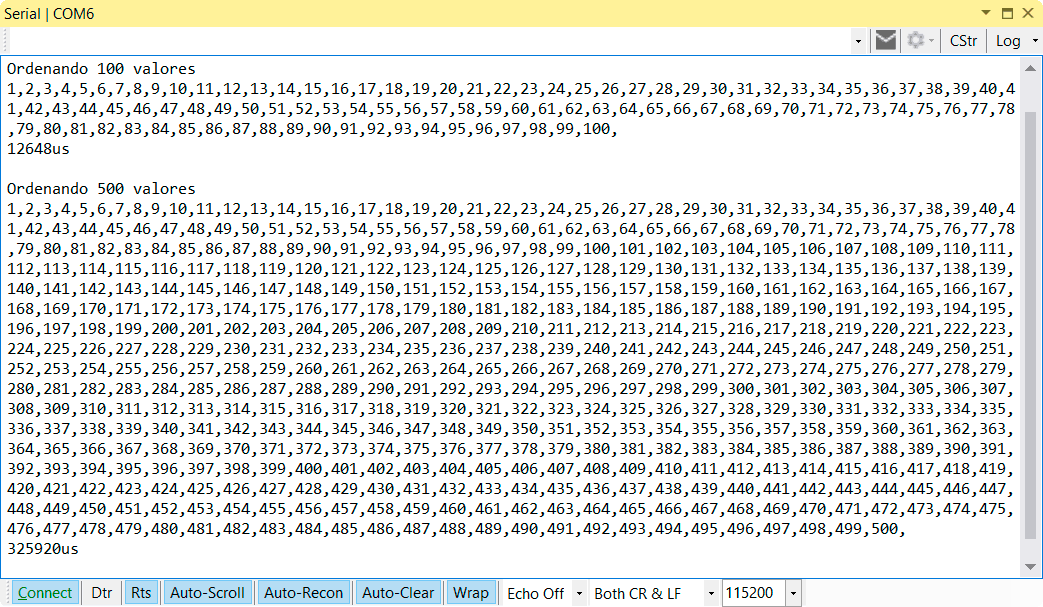 
The time obtained is 12.65ms for the sample of 100 elements, and 325.92ms for the sample of 500 elements. As we can see, sorting 5 times more elements costs 25.75 times more, which fits with the O(n^2) we mentioned (math still works and the world can keep turning).
In the next post, we will implement the QuickSort algorithm, a much more efficient sorting algorithm.
Download the code
All the code in this post is available for download on Github. 