Hoy vamos la corrección Gamma, un aspecto fundamental a tener en cuenta a la hora de trabajar con fuentes de iluminación a la que queremos variar la intensidad con un procesador como Arduino.
Supongamos el sencillo caso de un LED al que queremos variar la iluminación. Muy fácil ¿verdad? Simplemente usamos una señal PWM para encender y apagar el LED como vimos en el último ejemplo de esta entrada.
Con esto estamos apagando el LED durante un cierto porcentaje del tiempo, tan rápido que no podemos verlo. La iluminación, es de esperar, debería variar en la misma relación que el tiempo que está apagado el LED (spoiler, va a ser que no).
Si hacéis este sencillísimo experimento, encendiendo el LED según una función triangular, veréis que la respuesta del LED no es en absoluto lineal. De hecho, vuestro LED estará “prácticamente todo el rato” encendido, y la bajada y la subida de iluminación se producirá en un intervalo de tiempo muy pequeño.
¿Cómo puede ser esto? ¿Qué está pasando aquí? Ah, amigo… por de ahí viene la corrección Gamma.
La corrección Gamma
Lo que está pasando es que tu ojo-cerebro te están engañando. Tu sistema de percepción visual está diseñado para funcionar en una gran un alto rango y ser especialmente sensible a cambios de poca luminosidad.
Aun asumiendo que la respuesta de tu emisor es lineal (que, en muchos casos, podremos asumir como cierto) es tu percepción de la luz la que no es lineal respecto a la cantidad de luz que percibe.
Es decir, cuando tu “ojo-cerebro” ve un LED encendido al 50% (medio encendido o medio apagado, depende de lo optimista que seas) tu percepción no es “que brilla el 50%“.
La forma de percepción visual humana sigue una forma aproximadamente potencial. Algo similar a la curva naranja en la siguiente gráfica.
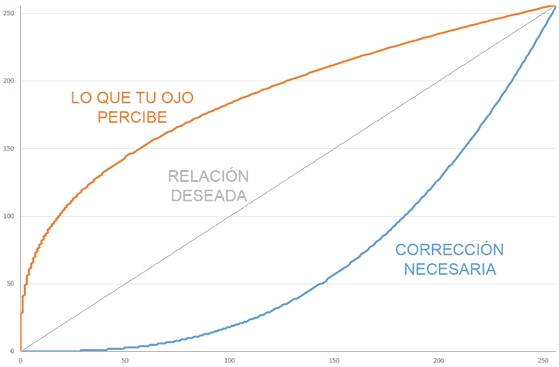
Para que la percepción coincida con el valor que deseamos (curva gris, totalmente lineal), necesitamos aplicar una corrección a los valores que aplicamos a la fuente de luz.
Esta corrección es lo que denominamos corrección Gamma y está representado en la gráfica anterior por la curva azul.
¿Demasiado raro? Bueno, así es como funciona tu cerebro.
Un ejemplo numérico
Por si aún te parece demasiado raro y para mostrar cómo de importante es el efecto de la corrección Gamma vamos a intentar ilustrarlo con un pequeño ejemplo numérico.
Supongamos que quieres encender un LED al 30% de iluminación aplicando un PWM entre 0 a 255. Lo “lógico” sería aplicar al PWM un valor de 0,3 * 255, es decir, en torno a 77.
Pero, si miramos la curva de percepción (naranja) con un valor de 77 percibirías una iluminación en torno al 65%. ¡Más del doble de lo que esperabas!
Para obtener una relación realmente en torno al 30% de la iluminación, deberías aplicar un valor de 8 (sí, solo 8 sobre 255). Como veis, la diferencia entre aplicar o no la corrección Gamma es enorme.
Esto resulta incluso más importante al trabajar con luces o tiras LED RGB. Si no tenemos en cuenta la corrección Gamma el color obtenido será totalmente diferente al que pretendíamos obtener.
Aplicar corrección Gamma en Arduino
Afortunadamente, aplicar la corrección Gamma en un procesador como Arduino es muy sencilla. Simplemente debemos corregir el valor que vamos a enviar al PWM (o al controlador que estemos usando).
Una forma de hacerlo es emplear una tabla con las correcciones que recoge los valores de corrección gamma necesarios para un valor de 8bits.
const static uint8_t PROGMEM GammeTable8[] = {
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2,
2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5,
5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 10,
10, 10, 11, 11, 11, 12, 12, 13, 13, 13, 14, 14, 15, 15, 16, 16,
17, 17, 18, 18, 19, 19, 20, 20, 21, 21, 22, 22, 23, 24, 24, 25,
25, 26, 27, 27, 28, 29, 29, 30, 31, 32, 32, 33, 34, 35, 35, 36,
37, 38, 39, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 50,
51, 52, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 66, 67, 68,
69, 70, 72, 73, 74, 75, 77, 78, 79, 81, 82, 83, 85, 86, 87, 89,
90, 92, 93, 95, 96, 98, 99,101,102,104,105,107,109,110,112,114,
115,117,119,120,122,124,126,127,129,131,133,135,137,138,140,142,
144,146,148,150,152,154,156,158,160,162,164,167,169,171,173,175,
177,180,182,184,186,189,191,193,196,198,200,203,205,208,210,213,
215,218,220,223,225,228,231,233,236,239,241,244,247,249,252,255 };
uint8_t CorrectGamma_Table8(uint8_t value)
{
result = pgm_read_byte(&GammeTable8[value]);
}Que en el código usaríamos para corregir los valores antes de enviar al emisor, por ejemplo, al escribir el PWM o antes de enviarlo al controlador.
analogWrite(pin, CorrectGamma_Table8(PWM));Esta tabla se guarda en la memoria de flash, ocupando 256 bytes. Lo cuál es bastante asumible, y tiene la ventaja de que el cálculo de la corrección es muy rápida.
Otra opción es emplear aritmética de enteros para ajustar una ecuación a la relación gamma. Evitamos usar números en coma flotante para evitar el cálculo que supone. Así, llegamos a la siguiente función.
uint8_t CorrectGamma8(uint8_t value)
{
return (((45 * ((unsigned long)value + 1) + 3488) * ((unsigned long)value + 1) - 136379) * ((unsigned long)value + 1) + 1305350) / 3722130;
}Que, por ejemplo, usaríamos así.
analogWrite(pin, CorrectGamma8(PWM));Los resultados obtenidos son similares a los obtenidos al usar la tabla. Este método tiene la ventaja de ocupar menos memoria aunque, por contra, es levemente más lenta (pero muy poco).
Corrección Gamma en una Librería
¿Y si lo metemos todo en una librería? Por supuesto que sí. Aquí tenéis la librería CorrectionGamma, una librería Open Source para Arduino que dispone de los dos métodos que hemos visto en esta entrada para poderlos usar de forma cómoda y sencilla.