Cómo sumar números en binario

La suma o adición es una operación aritmética fundamental. Por supuesto, en binario no no iba a ser diferente, y sumar números binarios es una de las operaciones más frecuentes que vamos a realizar.

Afortunadamente, no son muy diferentes de sus equivalentes decimales. De hecho, en binario es incluso más sencilla. Simplemente vamos a sumar dígito a dígito de derecha a izquierda, teniendo en cuenta los acarreos.

También es importante que, si estamos trabajando con números binarios de tamaño fijo, contemplemos el desbordamiento y subdesbordamiento.

Por último, en el caso de restas también deberías saber si estáis trabajando con números unsigned o signed.

Suma binaria

La suma binaria es una operación básica en el sistema binario. Es similar a la suma en el sistema decimal, pero se realiza con solo dos dígitos 0 y 1.

El resumen del proceso es el siguiente:

• Se comienza sumando los bits desde la derecha y se continúa hacia la izquierda
• Si la suma de dos bits es 1 o 0, se escribe el resultado debajo de los bits y se continúa
• Si la suma es 2, entonces se escribe un 0 y se lleva un 1 al siguiente bit de mayor peso

Acarreo (Carry)

En la suma binaria, un “acarreo” (carry) ocurre cuando la suma de dos bits produce un resultado que necesita ser “llevado” a la siguiente posición de bits.

Esto sucede cuando la suma de dos bits es igual a 2, es decir, cuando ambos bits que sumamos son 1. En este caso, el resultado es 0 y el acarreo supone sumar 1 cuando se suma al siguiente bit más significativo.

Ejemplo de suma binaria

Por ejemplo, para sumar los números binarios 1011 (11 en decimal) y 1101 (13 en decimal)

  1011
+ 1101
______
 11000

El resultado es 11000, que es igual a 25 en decimal.

  10101
+    11
______
 11000

Cómo sumar rápido en binario

La suma en binario es bastante sencilla. Sin embargo los números binarios generalmente son muy largos por lo que se hace… pesadita.

Normalmente no es una operación que tengáis que hacer a mano. Pero, si alguna vez tenéis que hacerla, normalmente porque a vuestro profesor le apetece, que sepáis que formas muy rápidas de hacer la suma.

De hecho, es facilísimo y muy rápido sumar números binarios. Empecemos analizando lo que nos vamos a encontrar. Primero supongamos que no estamos llevando acarreo.

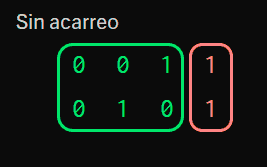
• Si ambos son 0, el resultado es 0
• Si uno es 0 y el otro 1 (o viceversa) “engranan”, y hacen un 1
• El único dificil escuando tenemos 1 y 1, que tenemos acarreo.

Ahora veamos que pasa cuando sí llevamos acarreo.

Aquí lo interesante es ver que, cuando llevamos acarreo, todas las combinaciones desbordan, excepto 0 con 0.

Es decir, una vez que “se me activa” el acarreo, el 1 que me llevo no puede bajar hasta que encuentre 0 y 0.

Ejemplo

Vamos a verlo con un ejemplo. Supongamos que queremos sumar estos dos números binarios de 12 bits.

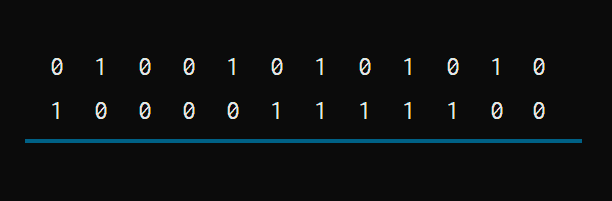
Empezamos por la derecha, y buscamos combinaciones 1 con 1. Aquí será que se active el acarreo.

A continuación, seguimos buscando hasta que encontremos un 0 con 0. Ahí es donde el acarreo podrá bajar

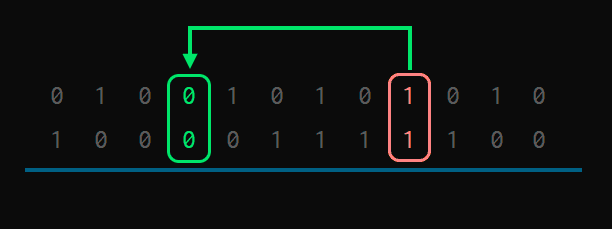
Al final es cómo si los 1-1 generan un 10. El 0 se queda en el sitio, y el 1 se vaaaa y se vaaaa hasta que encuentra un 0-0 donde poder bajar.

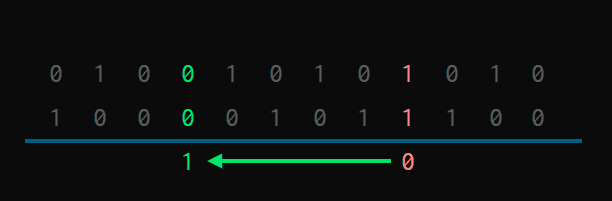
Ahora, simplemente tenemos que rellenar los bloques que hemos definido. En los bloques sin acarreo, aplicamos las normas normales.

• 0-0 suma 0
• 0-1 o 1-0, engrana uno con otro, y da 1

O, dicho de otra forma, en los bloques sin acarreo “mandan los 1“.

Ahora llegamos al siguiente bloque, que es con acarreo. Aquí “mandan los 0”. Si hay un 0 en los bit que estamos sumando, el resultado es 0. Si no 1.

Y seguiríamos cambiando entre bloque con acarreo, bloque sin acarreo, hasta que nos quedemos sin número.

Por último, también podéis verlo como que los bloques sin acarreo son XOR, y los de con acarreo NXOR.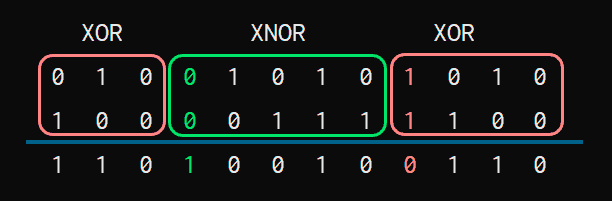

Que es menos práctico para operar, pero os permite usar el memotécnico de Hamlet de “Ser o NoSer”, para que dentro de muuuuchos años os sigáis acordando de que la sumas binarias se hacen en bloques XOR y NXOR:

Bonus: Cómo sumar 1 rápidamente en binario

Bonus especial, cómo sumar rápidamente 1 a un número binario. Una operación muy sencilla, pero que como es muy habitual conviene saber hacerla.

Afortunadamente, sumar 1 en binario “está tirado”. Simplemente

• Recorrer el número binario desde la derecha
• Buscas el primer 0 que encuentres, y lo cambias por 1
• Desde esa posición, hacía la derecha, todo 0s.

Por ejemplo, si tuviéramos que sumar 1 a 1000011111

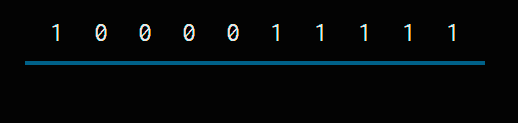
Buscamos el primer 0

Lo cambiamos por 1 y, de ahí para la derecha, todo 0.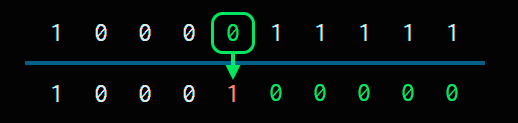

Así que el resultado es 1000100000. Como veis sumar uno es rapidísimo.