En la entrada anterior vimos de forma intensiva el filtro exponencial EMA aplicado a filtrado de paso bajo y paso alto. En esta entrada vamos a profundizar en el tema y extenderlo a filtros paso banda y filtros stop banda.
Para recapitular, recordemos que una señal puede ser considerada como una suma de componentes frecuenciales. Un filtro de paso bajo ideal (que es imposible de obtener en el mundo real) dejaría pasar los componentes por debajo de una frecuencia de corte (Fc). Por su parte, un filtro de paso alto ideal dejaría pasar los componentes por encima de una frecuencia de corte.
Los filtros de tipo paso banda y stop banda requieren dos frecuencias de corte que, de forma genérica, denominaremos frecuencia de corte inferior (Fci) y frecuencia de corte superior (Fcs).
Un filtro de paso banda ideal deja pasar únicamente las frecuencias superiores al corte inferior e inferiores al corte superior, es decir, los componentes frecuenciales en una banda entre ambas frecuencias de corte (Fci a Fcs)
Los filtros de paso tienen una amplia aplicación en electrónica. Los usáis diariamente cada vez que usáis un aparato que “sintonice” una señal. Eso incluye todas las formas de comunicación, desde radio, televisión, móvil, Wifi, entre una casi infinita cantidad de aplicaciones.
Por su parte el filtro de stop banda es el caso opuesto, es decir, elimina los componentes comprendidos entre ambas frecuencias de corte, por lo que únicamente deja pasar las frecuencias de -∞ a Fci y de Fcs a +∞.
Si bien no son tan frecuentes, igualmente tienen un enorme campo de aplicación cuando queremos eliminar una señal de frecuencia conocida. Por ejemplo, podemos eliminar las frecuencias de corriente alterna, filtrar las vibraciones de una máquina girando a unas revoluciones conocidas, o eliminar el parpadeo en sensores ópticos y cámaras originados por las luces artificiales alimentadas con corriente alterna.
Generar un filtro de paso banda y stop banda
Para generar un filtro de paso banda o stop banda generalmente partimos de un filtro de paso bajo y obtenemos el resto mediante operaciones con la señal original. Los resultados serían análogos partiendo de un filtro de paso alto, pero los algoritmos para generar directamente un filtro de paso alto son mucho menos frecuentes que los de paso bajo.
Recordemos que si dispusiéramos de nuestro imaginario (y a esta altura casi famoso) filtro de paso bajo ideal, generar un filtro de paso alto sería tan sencillo como restar a la señal original el filtro de paso bajo.
Para visualizarlo, imaginemos el espectro de la señal con sus componentes frecuenciales de -∞ a +∞. El filtro de paso bajo deja pasar únicamente las frecuencias inferiores a la frecuencia de corte (Fc), es decir, las frecuencias de -∞ a Fc.
Por tanto, restar al espectro el resultado del filtro paso baja deja pasar las frecuencias de Fc a +∞ lo que corresponde, precisamente, con el comportamiento de un filtro de paso alto.
Por extensión, para generar un filtro de paso banda únicamente tenemos que restar al filtro de paso bajo de la frecuencia de superior el filtro de paso bajo de la frecuencia inferior.
El filtro de paso bajo superior dejara las frecuencias de -∞ a Fcs, y el filtro paso bajo inferior las frecuencias de -∞ a Fci, por lo que restar ambos valores dejará las frecuencias de Fci a Fcs, que es justamente lo que queremos.
Finalmente, para obtener el filtro de stop banda únicamente tenemos que restar a la señal original el filtro del paso banda, lo que dejará pasar las frecuencias de -∞ a Fci y Fcs a +∞.
En este punto cabe recordar que la mayor parte de lo explicado aquí es de aplicación para gran variedad de filtros. En esta entrada usamos el filtro exponencial EMA porque es ampliamente empleado y obtiene buenos resultados con una implementación sencilla y alta eficiencia computacional.
Sin embargo, cualquier algoritmo que “suavice” una señal puede ser empleado como filtro de paso bajo (con mejores o peores características) y, por tanto, es susceptible de dar origen a un filtro de paso alto, paso banda, y stop banda.
Resultados del filtro paso banda
Como dijimos en la entrada anterior, en el filtro de tipo exponencial la cantidad de suavizado se controla a través del factor alpha. No es sencillo encontrar una relación sencilla con la frecuencia de corte, entre otras cosas, porque la frecuencia de muestreo es desconocida y variable.
Lo que sí sabemos es que cuanto menor sea el factor alpha mayor será el suavizado de la señal, y por tanto, menor la frecuencia de corte. Recordar que, como punto negativo, también será mayor el retraso entre la señal filtrada y la señal original.
En un filtro paso banda y stop banda tendremos dos factores alpha que denominaremos Low y High que corresponden, respectivamente, con la frecuencia de corte inferior y superior.
A continuación veremos el efecto de estos factores con los resultados del filtro paso banda para distintas combinaciones de alpha Low y High aplicados a la misma señal.
Estos son los resultados para un alpha Low de 0.025 y alpha High de 0.5. Observar que el filtro inferior ha eliminado el bias pasadas unas pocas oscilaciones, mientras que el filtro superior ha suavizado parte del ruido de alta frecuencia
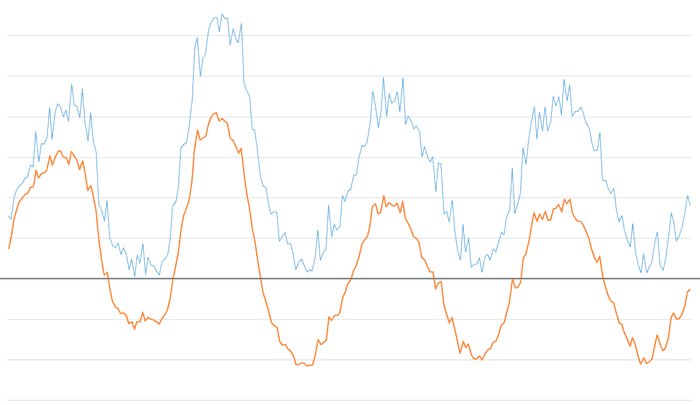
Si disminuimos el factor alpha high a 0.3, manteniendo el low a 0.025, vemos que se elimina la mayor parte del ruido de alta frecuencia.
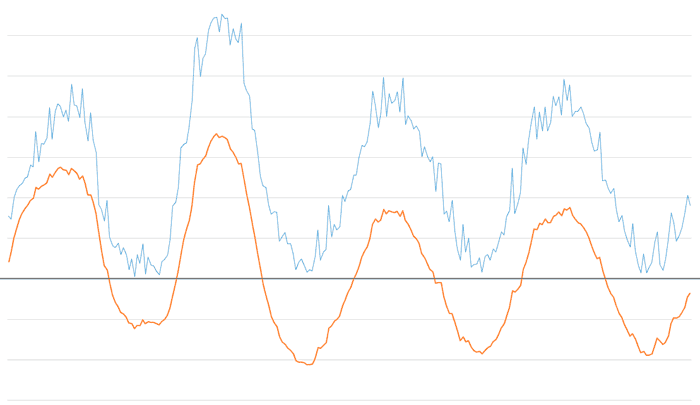
Y si disminuimos aún más el factor de alpha high a 0.15 veremos que hemos eliminado todos los componentes excepto los armónicos fundamentales de la señal del ejemplo.
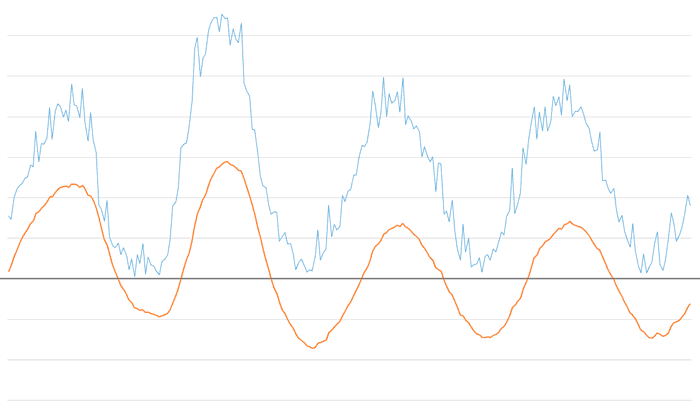
Es decir, en un único filtro hemos eliminado el ruido de alta frecuencia y el bias de la señal. ¿No está mal para un filtro tan sencillo, verdad?
Filtro de paso banda y stop banda en Arduino
Aquí tenemos una implementación sencilla de un filtro de paso banda y stop banda exponencial (EMA). En el ejemplo vamos a filtrar una serie de integer desordenados que simulan una señal como la que podríamos obtener al realizar una medición. Accedemos a estos valores a través de la función GetMeasure(), que simula el proceso de adquisición de datos.
Los resultados se muestran por puerto serie. Si empleáis el Serial Plotter del IDE Standard podréis ver los resultados gráficamente de forma sencilla.
float EMA_ALPHA_LOW = 0.025;
float EMA_ALPHA_HIGH = 0.1;
int EMA_LP_LOW = 0;
int EMA_LP_HIGH = 0;
int EMA_BP = 0;
int EMA_BS = 0;
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index-1];
}
void setup()
{
Serial.begin(115200);
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
int filteredBP = EMABandPassFilter(value);
int filteredBS = EMABandStopFilter(value);
Serial.print(value);
Serial.print(",");
Serial.print(filteredBP);
Serial.print(",");
Serial.println(filteredBS);
}
}
void loop()
{
delay(10000);
}
int EMABandPassFilter(int value)
{
EMA_LP_LOW = EMA_ALPHA_LOW * value + (1 - EMA_ALPHA_LOW) * EMA_LP_LOW;
EMA_LP_HIGH = EMA_ALPHA_HIGH * value + (1 - EMA_ALPHA_HIGH) * EMA_LP_HIGH;
EMA_BP = EMA_LP_HIGH - EMA_LP_LOW;
return EMA_BP;
}
int EMABandStopFilter(int value)
{
EMA_LP_LOW = EMA_ALPHA_LOW * value + (1 - EMA_ALPHA_LOW) * EMA_LP_LOW;
EMA_LP_HIGH = EMA_ALPHA_HIGH * value + (1 - EMA_ALPHA_HIGH) * EMA_LP_HIGH;
EMA_BP = EMA_LP_HIGH - EMA_LP_LOW;
EMA_BS = value - EMA_BP;
return EMA_BS;
}Los resultados en el Serial Plotter del IDE Estándar serán los siguientes,
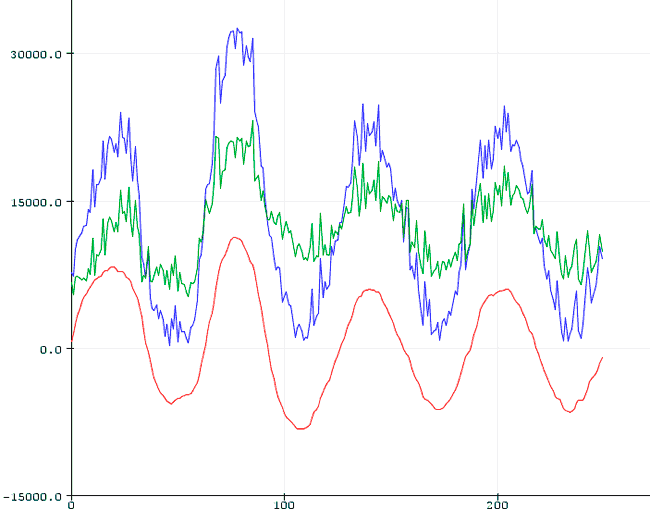
Filtro de paso banda y stop banda en una librería
¿Y si lo metemos en una librería para que sea más cómodo de usar? Por supuesto que sí, aquí una librería Double EMA Filter para Arduino. ¡A disfrutarlo!
Descarga el código
Todo el código de esta entrada está disponible para su descarga en Github.