Continuamos con los filtros digitales como forma de mejorar los valores obtenidos en las mediciones de sensores en nuestros proyectos de electrónica y robótica con Arduino.
Hasta ahora hemos visto el filtro de media móvil y el filtro exponencial EMA para filtrado paso bajo y paso alto y EMA doble para filtro paso banda y stop banda. Estos filtros son sencillos y eficientes de implementar pero tienen la desventaja de que son poco robustos/estables ante la aparición de puntos espurios (puntos que se desvían mucho del valor real).
Esto es debido a que ambos filtros (media móvil y filtro exponencial) se basan en la media como estimador de tendencia. Como ya vimos al hablar del cálculo de la mediana rápido en Arduino, la media es un estimador de tendencia poco robusto. Su popularidad se debe, en gran medida, a la sencillez de cálculo y a que es una función que podemos manipular y derivar.
El mejor ejemplo para ilustrar la inestabilidad de la media es el comportamiento ante espurios. Un único punto anómalo puede provocar una gran desviación en la media arruinando toda una serie de mediciones, loque muestra la falta de robustez de la media como estimador de tendencia.
Afortunadamente la media no es el único estimador de tendencia. Aquí la estadística viene al rescate, en concreto la rama de la estadística robusta, que es la encargada de realizar cálculos de mayor estabilidad que la estadística tradicional. Y precisamente la estadística robusta emplea como indicador de tendencia la mediana.
En esta entrada nos centraremos en implementar un filtro de mediana móvil de forma eficiente, y lo suficientemente ligero para que pueda caber en un microprocesador como Arduino.
El filtro mediana móvil
De forma similar al filtro de media móvil, el filtro de mediana móvil define una ventana de N elementos, que recoge las últimas N mediciones. El valor del filtro es la mediana de los valores contenidos en la ventana.
Aumentar el tamaño de la ventana aumenta el suavizado de la señal pero añade un retraso a la señal (como ocurría en el filtro media móvil y EMA) ya que es necesario “esperar” al muestreo de más puntos.
El tamaño de la ventana dependerá de las características de nuestro sistema y de la señal a filtrar, pero son habituales tamaños de 5 a 11. En general se prefieren tamaños de ventana impares para evitar tener que promediar entre dos muestras, lo cual eliminaría parte de la capacidad de filtrado de la mediana.
Un filtro de mediana móvil es un instrumento muy útil y ampliamente empleado en electrónica. Son muy empleados en sistemas de adquisición de datos y captación de sensores para la eliminación de ruido, por ejemplo, en giroscopios y acelerómetros.
El filtro de mediana móvil presenta mejores características en el filtrado de ciertos tipos de señal, especialmente las que presentan espurios o ante el ruido sal y pimienta (ruido que hace que puntos vayan al mínimo o máximo posible).
Por contra, emplear la mediana como filtro también tiene sus desventajas. La más evidente es que, en general, computacionalmente es un cálculo más costoso. Normalmente se considera que el cálculo de la mediana implica la ordenación de todos los valores contenidos, lo cual demostramos que no es cierto al hablar del cálculo de la mediana
Por otro lado, el filtro de mediana únicamente puede devolver puntos muestreados, por lo que perdemos la capacidad de “interpolación” (submuestreo) que podemos obtener con otros filtros. Esto produce que las señales filtradas sean “angulosas” y presenten saltos discretos.
No obstante es posible mejorar el comportamiento combinando el filtro de mediana móvil con un filtro exponencial EMA, teniendo en cuenta que el factor de ambos filtros se va a acumular. Por tanto deberemos llegar a un compromiso, reduciendo el tamaño de la ventana y el alpha del EMA para no disparar el retraso global.
Resultados del filtro de mediana
Para ilustrar el comportamiento del filtro mediana móvil vamos a mostrar los resultados para una misma señal de entrada simulada y distintos tamaños de ventana.
La primera figura muestra el filtro mediana para un tamaño de ventana de 3. Vemos que ha quitado la mayoría de los “picos” de la señal, lo que se corresponde con lo que hemos comentado sobre la capacidad del filtro de mediana para la eliminación de espurios y ruido.
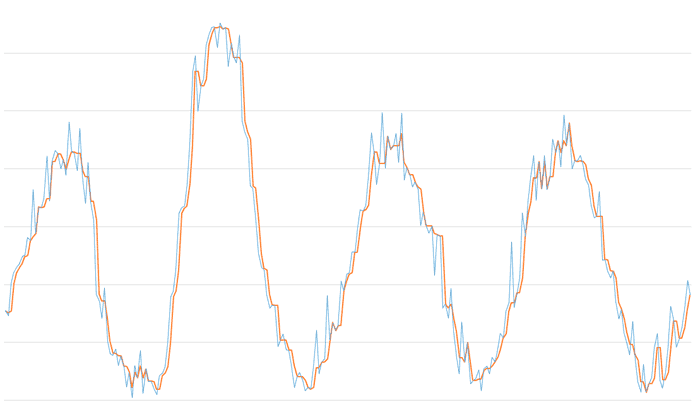
No obstante, un tamaño de ventana de 3 es normalmente escaso ya que de coincidir dos puntos anómalos el filtro sólo sería capaz de absorber/eliminar uno.
La siguiente gráfica muestra el resultado para una ventana de tamaño 5. Con una ventana mayor el filtro de mediana aumenta la fortaleza ante el ruido. Sin embargo, comprobamos el comportamiento anguloso y “a saltos” que comentábamos antes.
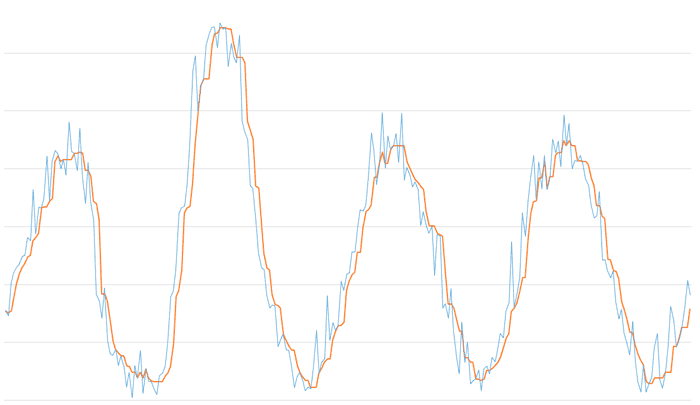
La siguiente gráfica muestra el resultado para una ventana de tamaño 11. La señal filtrada aumenta su suavizado, pero el retraso empieza a hacerse evidente.
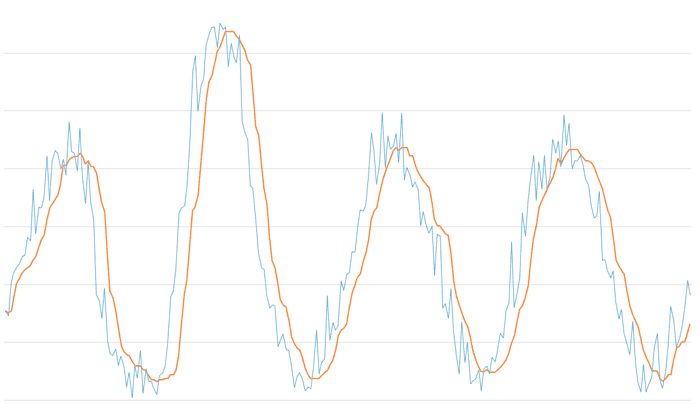
Finalmente, la última gráfica muestra la combinación de un filtro de mediana con un tamaño de ventana de 3 con un filtro exponencial EMA de Alpha 0.3
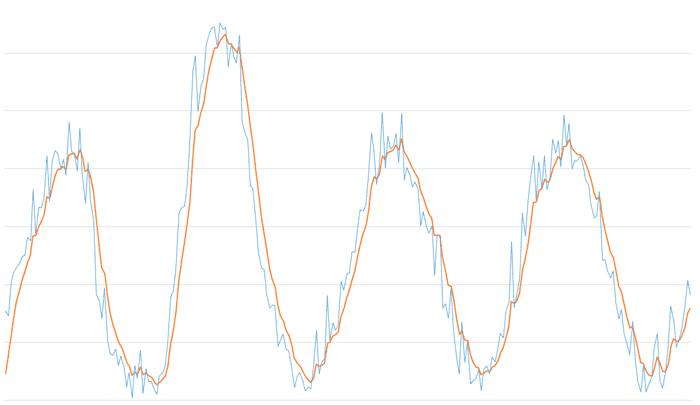
Vemos que la combinación de un filtro de mediana con una ventana reducida (5 sería un buen valor) junto con un EMA de alpha moderado aporta el filtro de ruido y espurios de la mediana junto con la suavidad y submuestreo que aporta el EMA, a la vez que mantenemos el retraso en valores aceptables.
Implementar un filtro mediana en Arduino
Vamos a probar tres implementaciones distintas para la implementación de un filtro de mediana móvil. Ya os adelanto (¡spoiler!) que la más eficiente, lógicamente, va a ser la última. Pero vamos a presentar las tres, sobre todo para aquellos implementando tozudamente el filtro mediana con un algoritmo de ordenación simple :).
Filtro mediana con Quick Sort
La primera opción es ordenar los valores de la ventana con un algoritmo de ordenación. En la entrada sobre ordenación con QuickSort ya demostramos que es mucho más rápido que otras alternativas como el famoso (e ineficiente) método de la burbuja o el algo menos famoso (y no mucho menos famoso) método inserción.
Por tanto, sólo vamos probar nuestro algoritmo Quick Sort. Una implementación ligera del filtro mediana con Quick Sort sería la siguiente.
const int windowSize = 3;
int buffer[windowSize];
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
#define MEDIAN(a, n) a[(((n)&1)?((n)/2):(((n)/2)-1))];
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
int elementCount;
float AddValue(int value)
{
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
memcpy(buffer, medianBuffer, sizeof(medianBuffer));
QuickSortAsc(buffer, 0, elementCount - 1);
int med = MEDIAN(medianBuffer, windowSize);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
void QuickSortAsc(int* arr, const int left, const int right)
{
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
while (i <= j)
{
while (arr[i]<pivot) i++;
while (arr[j]>pivot) j--;
if (i <= j)
{
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
if (left<j)
QuickSortAsc(arr, left, j);
if (i<right)
QuickSortAsc(arr, i, right);
}Filtro mediana con Quick Median
La siguiente evolución es que, como vimos en la entrada sobre calcular la mediana rápido en Arduino, existen algoritmos más eficientes para calcular la mediana que no requiren la ordenación completa del vector.
En la entrada ensayamos distintos algoritmos, optando finalmente por el algoritmo Quick Select modificado por Wirth por su alta eficiencia e implementación relativamente sencilla, apropiada para un procesador como Arduino.
Por tanto, vamos a probar a implementar el filtro de mediana mediante el algoritmo Quick Select Wirth para el cálculo de la mediana de la ventana. Una desventaja del método es que el algoritmo Quick Select modifica el vector, por lo que tendremos que copiar la ventana en un buffer intermedio para el cálculo.
La implementación sería la siguiente.
const int windowSize = 33;
int buffer[windowSize];
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
#define ELEM_SWAP(a,b) { int t=(a);(a)=(b);(b)=t; }
#define MEDIAN(a,n) kth_smallest(a,n,(((n)&1)?((n)/2):(((n)/2)-1)))
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
int elementCount;
float AddValue(int value)
{
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
memcpy(buffer, medianBuffer, sizeof(medianBuffer));
int med = MEDIAN(medianBuffer, elementCount);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
int kth_smallest(int a[], int n, int k)
{
int i, j, l, m;
int x;
l = 0;
m = n - 1;
while (l<m)
{
x = a[k];
i = l;
j = m;
do {
while (a[i]<x) i++;
while (x<a[j]) j--;
if (i <= j)
{
ELEM_SWAP(a[i], a[j]);
i++;
j--;
}
} while (i <= j);
if (j<k) l = i;
if (k<i) m = j;
}
return a[k];
}Filtro mediana Quick Median Filter
El último algoritmo probado es el algoritmo propuesto por Phil Ekstrom en noviembre 2000. Ekstrom usa una combinación de buffer circular y linkedlist para mejorar la eficiencia del filtro de mediana, especialmente para tamaños de ventana grandes.
De forma similar a la motivación de emplear una buffer circular para calcular el filtro de media móvil, el algoritmo de Ekstrom encuentra su origen en que añadir un nuevo valor y eliminar el más antiguo a la ventana no modifica sustancialmente su estructura. En particular, no es necesario procesarla por completo.
Ekstrom emplea un buffer circular para almacenar los elementos de la ventana según su antigüedad. Por otro lado, cada elemento contiene un puntero al siguiente elemento de menor tamaño, formando una linkedlist.
Añadir un nuevo elemento en el buffer circular e insertar un elemento en la linkedlist es inmediato. El único coste computacional real es encontrar el punto de inserción, para lo cual es necesario recorrer la linkedlist.
La implementación resulta sencilla y adecuada para un microprocesador como Arduino. No obstante es posible mejorar su eficiencia, al igual que existen algoritmos con mejor eficiencia, a costa de un mayor uso de memoria.
#define MEDIAN_FILTER_WINDOW 7
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
int med = medianFilter(value);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(values[iCount]);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
#define STOPPER 0
uint16_t medianFilter(uint16_t value)
{
struct node
{
struct node *next;
uint16_t value;
};
static struct node buffer[MEDIAN_FILTER_WINDOW] = { 0 };
static struct node *iterator = buffer;
static struct node smaller = { nullptr, STOPPER };
static struct node bigger = { &smaller, 0 };
struct node *successor;
struct node *accessor;
struct node *accessorPrev;
struct node *median;
uint16_t i;
if (value == STOPPER)
value++;
if ((++iterator - buffer) >= MEDIAN_FILTER_WINDOW)
iterator = buffer;
iterator->value = value;
successor = iterator->next;
median = &bigger;
accessorPrev = nullptr;
accessor = &bigger;
if (accessor->next == iterator)
accessor->next = successor;
accessorPrev = accessor;
accessor = accessor->next;
for (i = 0; i < MEDIAN_FILTER_WINDOW; ++i)
{
if (accessor->next == iterator)
accessor->next = successor;
if (accessor->value < value)
{
iterator->next = accessorPrev->next;
accessorPrev->next = iterator;
value = STOPPER;
};
median = median->next;
if (accessor == &smaller)
break;
accessorPrev = accessor;
accessor = accessor->next;
if (accessor->next == iterator)
accessor->next = successor;
if (accessor->value < value)
{
iterator->next = accessorPrev->next;
accessorPrev->next = iterator;
value = STOPPER;
}
if (accessor == &smaller)
break;
accessorPrev = accessor;
accessor = accessor->next;
}
return median->value;
}Bonus: Filtro mediana de tamaño 3
Si estamos usando un tamaño de ventana 3 el filtro admite una implementación mucho más sencilla y eficiente.
const int windowSize = 3;
int medianBuffer[windowSize];
int* medianBufferAccessor = medianBuffer;
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*medianBufferAccessor = value;
medianBufferAccessor++;
if (medianBufferAccessor >= medianBuffer + windowSize)
medianBufferAccessor = medianBuffer;
}
float AddValue(int value)
{
appendToBuffer(value);
}
void setup()
{
Serial.begin(115200);
float timeMean = 0;
for (int iCount = 0; iCount < valuesLength; iCount++)
{
int value = getMeasure();
long timeCount = micros();
AddValue(value);
int med = median3(medianBuffer);
timeCount = micros() - timeCount;
timeMean += timeCount;
Serial.print(value);
Serial.print(",");
Serial.println(med);
}
Serial.println(timeMean / valuesLength);
}
void loop()
{
}
int median3(int arr[])
{
if ((arr[0] <= arr[1]) && (arr[0] <= arr[2]))
return (arr[1] <= arr[2]) ? arr[1] : arr[2];
else if ((arr[1] <= arr[0]) && (arr[1] <= arr[2]))
return (arr[0] <= arr[2]) ? arr[0] : arr[2];
else
return (arr[0] <= arr[1]) ? arr[0] : arr[1];
}Comparación
Aquí tenemos el tiempo necesario para ejecutar los distintos algoritmos, para distintos tamaños de ventana. Todos ellos se han realizado en un Arduino Nano 16Mhz. Los resultados se muestran en us.
| Window | QuickSort | Wirth | Ekstrom | Directo |
|---|---|---|---|---|
| 3 | 23.28 | 23.02 | 14.14 | 5.29 |
| 5 | 44.03 | 32.67 | 18.02 | - |
| 7 | 64.83 | 42.37 | 22.37 | - |
| 9 | 94.34 | 53.15 | 26.83 | - |
| 11 | 115.94 | 64.86 | 30.83 | - |
| 33 | 403.73 | 189.25 | 80.78 | - |
Como vemos, el algoritmo de Ekstrom es mucho más rápido que el resto de alternativas, incluso habiendo empleado algoritmos muy rápidos para la ordenación (Quick Sort) y cálculo de la mediana (Quick Select Wirth).
Lógicamente, para un tamaño de ventana de 3 el algoritmo directo es mucho más rápido, pero normalmente no usaremos el tamaño de 3 porque como hemos comentado, es demasiado pequeño.
Para valores habituales de (de 5 a 11) el filtro de mediana con el algoritmo de Ekstrom es del orden de 2 veces más rápido que el cálculo de la mediana con Quick Select, y 3 veces más rápido que la ordenación con Quick Select. Valores superiores de ventana proporciona diferencias superiores a favor de Ekstrom.
Filtro de mediana rápido en una librería
¿Y si limpiamos y mejoramos el código, y lo metemos en una librería para que sea más cómodo de usar? Por supuesto que sí, aquí una librería Median Filter para Arduino. ¡A disfrutarlo!
Descarga el código
Todo el código de esta entrada está disponible para su descarga en Github.