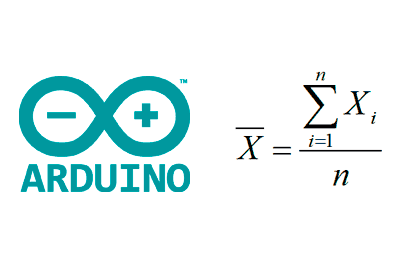En la entrada sobre muestreo múltiple en Arduino ya introdujimos que la reducción del ruido en las mediciones va a ser una constante (y casi una obsesión) en cualquiera de nuestros proyectos de electrónica y robótica. También vimos que la solución pasa por tomar varias mediciones y emplear un algoritmo para combinar las mediciones.
Vamos empezar con la aplicación de filtros propiamente dichos, entendiendo como filtro digital a un algoritmo que nos permite combinar varios puntos de una señal muestreada para obtener un valor con mayor significación que los puntos individuales.
Existen muchos filtros digitales posibles. En esta entrada vamos a ver el filtro de media móvil, un filtro digital ampliamente utilizado porque es intuitivo, fácil de implementar y rápido de calcular.
En el filtro de media móvil tomamos los últimos N valores recibidos (a los que denominaremos “ventana”) y calculamos su media. El resultado es una señal suavizada que elimina parte del ruido de alta frecuencia. El tamaño de la ventana tiene una gran influencia en el comportamiento del filtro, como veremos más adelante.
El filtro de media móvil es muy sencillo de implementar ya que el cálculo de la media únicamente requiere sumar los N elementos de la ventana y dividir para N.
La eficiencia del algoritmo mejora de forma sustancial al emplear un buffer circular. La motivación es que añadir un nuevo elemento a la ventana la suma se “poco” afectada. Únicamente es necesario restar el primer valor de la ventana y sumar el nuevo valor.
Empleando un buffer circular podemos calcular el nuevo valor filtrado sin necesidad de recorrer los N elementos de la ventana, lo que mejora la eficiencia del algoritmo respecto al tamaño de la ventana de O(n) a O(1).
Pese a las ventajas del filtro de media móvil, sobre todo en cuanto a eficiencia y sencillez, por supuesto también tiene sus desventajas, principalmente relacionadas con la debilidad del uso de la media como estimador de tendencia.
En particular, el filtro de media móvil es poco estable ante la aparición de puntos espurios (puntos anómalos muy alejados del valor real). En estos casos, resulta más conveniente emplear un filtro de mediana, o una combinación de ambos.
Influencia del tamaño de la ventana
El tamaño de la ventana condiciona el comportamiento del filtro. Un valor de 1 dejaría la señal inalterada. Cuanto mayor sea el tamaño, más grande será el suavizado de la señal.
Sin embargo, aumentar el tamaño de la ventana también tiene consecuencias negativas. Por un lado, podemos eliminar componentes de la señal en las que tenemos interés (variaciones auténticas de la señal y no solo ruido). Por otro, introduce un desfase entre la señal original y la señal filtrada, dado que necesitamos acumular N elementos antes de proporcionar un valor.
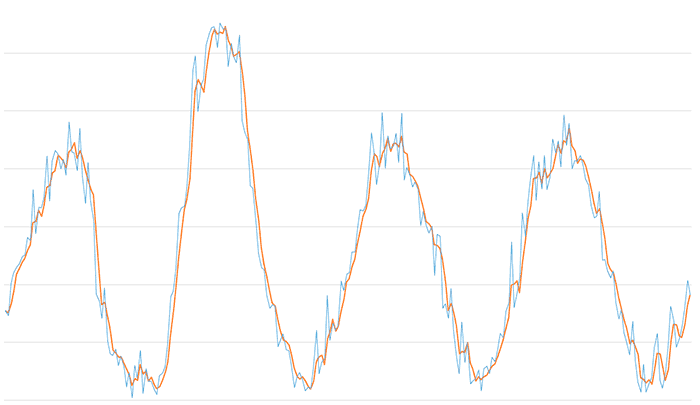
Aquí tenemos los resultados de un filtro de una misma señal para una ventana de tamaño 3,
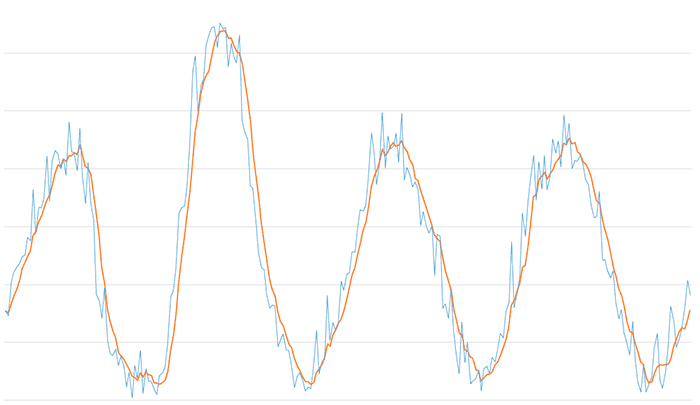
Para una ventana de tamaño 5,
Y para una ventana de tamaño 10,
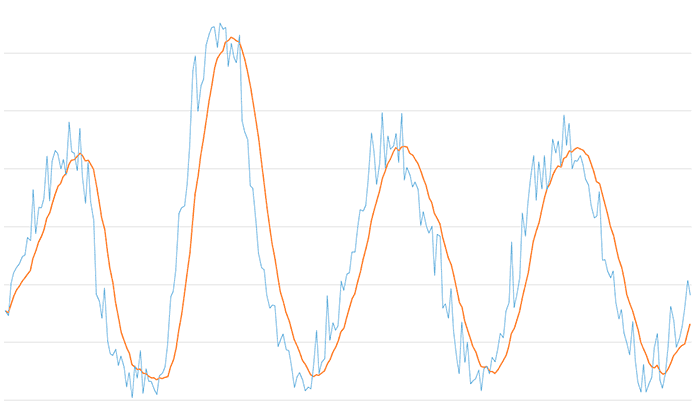
El valor adecuado para el tamaño de la ventana depende totalmente del tipo de señal que tengamos (cantidad de ruido, frecuencia, etc) y de nuestro sistema (frecuencia de muestreo, fiabilidad, etc). No obstante, son habituales valores entre 3 y 10.
Implementación en Arduino
Aquí tenemos una implementación ligera de un filtro de media móvil empleando un buffer circular para almacenar los N valores de la ventana.
En el ejemplo vamos a filtrar una serie de integer desordenados que simulan una señal como la que podríamos obtener al realizar una medición. Accedemos a estos valores a través de la función GetMeasure(), que simula el proceso de adquisición de datos.
const int windowSize = 5;
int circularBuffer[windowSize];
int* circularBufferAccessor = circularBuffer;
int values[] = { 7729, 7330, 10075, 10998, 11502, 11781, 12413, 12530, 14070, 13789, 18186, 14401, 16691, 16654, 17424, 21104, 17230, 20656, 21584, 21297, 19986, 20808, 19455, 24029, 21455, 21350, 19854, 23476, 19349, 16996, 20546, 17187, 15548, 9179, 8586, 7095, 9718, 5148, 4047, 3873, 4398, 2989, 3848, 2916, 1142, 2427, 250, 2995, 1918, 4297, 617, 2715, 1662, 1621, 960, 500, 2114, 2354, 2900, 4878, 8972, 9460, 11283, 16147, 16617, 16778, 18711, 22036, 28432, 29756, 24944, 27199, 27760, 30706, 31671, 32185, 32290, 30470, 32616, 32075, 32210, 28822, 30823, 29632, 29157, 31585, 24133, 23245, 22516, 18513, 18330, 15450, 12685, 11451, 11280, 9116, 7975, 8263, 8203, 4641, 5232, 5724, 4347, 4319, 3045, 1099, 2035, 2411, 1727, 852, 1134, 966, 2838, 6033, 2319, 3294, 3587, 9076, 5194, 6725, 6032, 6444, 10293, 9507, 10881, 11036, 12789, 12813, 14893, 16465, 16336, 16854, 19249, 23126, 21461, 18657, 20474, 24871, 20046, 22832, 21681, 21978, 23053, 20569, 24801, 19045, 20092, 19470, 18446, 18851, 18210, 15078, 16309, 15055, 14427, 15074, 10776, 14319, 14183, 7984, 8344, 7071, 9675, 5985, 3679, 2321, 6757, 3291, 5003, 1401, 1724, 1857, 2605, 803, 2742, 2971, 2306, 3722, 3332, 4427, 5762, 5383, 7692, 8436, 13660, 8018, 9303, 10626, 16171, 14163, 17161, 19214, 21171, 17274, 20616, 18281, 21171, 18220, 19315, 22558, 21393, 22431, 20186, 24619, 21997, 23938, 20029, 20694, 20648, 21173, 20377, 19147, 18578, 16839, 15735, 15907, 18059, 12111, 12178, 11201, 10577, 11160, 8485, 7065, 7852, 5865, 4856, 3955, 6803, 3444, 1616, 717, 3105, 704, 1473, 1948, 4534, 5800, 1757, 1038, 2435, 4677, 8155, 6870, 4611, 5372, 6304, 7868, 10336, 9091 };
int valuesLength = sizeof(values) / sizeof(int);
int getMeasure()
{
int static index = 0;
index++;
return values[index - 1];
}
int appendToBuffer(int value)
{
*circularBufferAccessor = value;
circularBufferAccessor++;
if (circularBufferAccessor >= circularBuffer + windowSize)
circularBufferAccessor = circularBuffer;
}
long sum;
int elementCount;
float mean;
float AddValue(int value)
{
sum -= *circularBufferAccessor;
sum += value;
appendToBuffer(value);
if (elementCount < windowSize)
++elementCount;
return (float) sum / elementCount;
}
void setup()
{
Serial.begin(115200);
for (int iCount = 0; iCount < valuesLength; iCount++)
{
float med = AddValue(getMeasure());
Serial.print(values[iCount]);
Serial.print(",\t");
Serial.println(med);
}
}
void loop()
{
}Si ejecutamos el código veremos el siguiente resultado del valor original y del valor filtrado.
Si empleáis el Serial Plotter del IDE estándar de Arduino podréis ver fácilmente la gráfica de los valores.
Filtro de media móvil en una librería
¿Y si lo metemos en una librería para que sea más cómodo de usar? Por supuesto que sí, aquí una librería MeanFilter para Arduino. ¡A disfrutarlo!
Descarga el código
Todo el código de esta entrada está disponible para su descarga en Github.